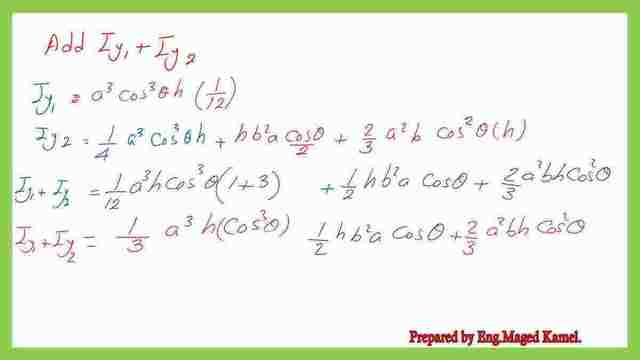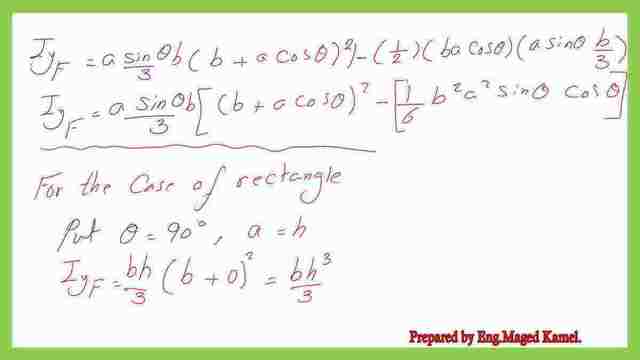Last Updated on January 2, 2026 by Maged kamel
Moment of inertia Iy for parallelogram.
Divide into areas and estimate the inertia of each area about the y-axis.
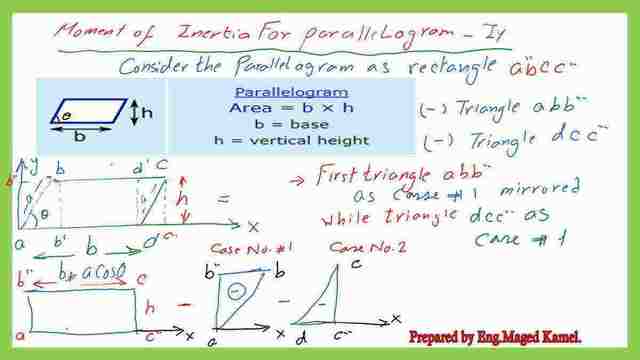
The post includes how to estimate the moment of inertia Iy for a parallelogram. The axis y passes through the left corner of the parallelogram and intersects with the base of the Parallelogram at Point a.
A parallelogram is a skewed rectangle with an angle=θ, between the base and the left side, when θ=90, the shape becomes a rectangle.
The area of the parallelogram is b*a, whereas the side length and the height are a and h = a*sinθ, respectively. To get the expression for Iy, we will divide the parallelogram into two triangles and a rectangle.
We will use the previously obtained data on the moment of inertia about the y-axis for the right-angled triangle and rectangle.
Iy for right-angle case-1, Iy for right-angle triangle case-2, and Iy for the rectangle. The sum of the inertia for the two triangles will be deducted from the inertia of the big triangle.
The inertia of the left triangle about the y-axis.
The left triangle has an upper base of (a* cos θ) and height h, the inertia for the y-axis will be estimated about an axis passing by the left corner point of the base of the parallelogram. It can be considered as the sum of Iy about the CG plus the Inertia value from the product of(A* x bar^2).
The expression for the inertia Iy for the left triangle can be simplified as shown in the next slide image.
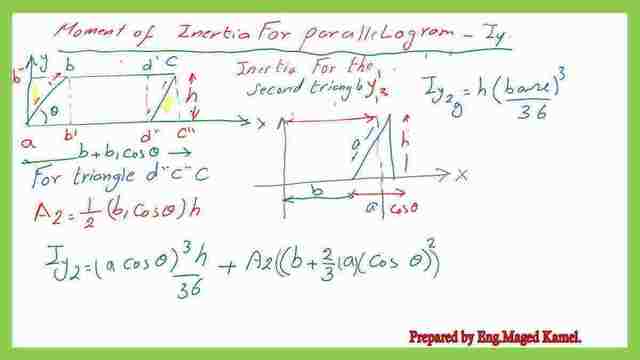
The inertia of the right triangle about the y-axis.
As for the right triangle, it has a bottom base of (a* cos θ) and a height of h, the inertia for the y-axis will be estimated about an axis passing by the CG point, then add the product of the area*x cg^2, where xcg is the distance from the Cg to the external Y-axis. Iy2 is the sum value shown in the next slide image.
More simplification is shown in the next slide image for Iy2. The detailed calculations for Iy for a parallelogram are shown in the next slide image.
We will add the inertia of the two triangles to get their sum, which will later be subtracted from the inertia Iy of the big triangle.
The steps for inertia Iy for the parallelogram.
The inertia of the big rectangle can be considered as the height* base^3/3, the left side of that rectangle coincides with the Y-axis.
The final value of the inertia Iy for the parallelogram is to be obtained by deducting the inertia of the two triangles from the Iy of the rectangle. The steps of estimation are shown in the following slide images. The common items can be cleared.
The final expression for inertia Iy for a parallelogram is shown in a similar form to the expression shown in the NCEES Handbook. For the rectangle, the value of Iy is 90 degrees.
When substituted into the equation for the inertia Iy of a parallelogram, we get the same expression for the inertia of a rectangle about the y-axis.
The value of the radius of gyration at the external corner for the parallelogram can be obtained by dividing Iy at the left edge by the area of the parallelogram. The expression for r^2y for the parallelogram is shown in the next slide image.
The steps for Inertia Iy for Parallelogram at the Cg.
The inertia Iy for the parallelogram at the Cg can be estimated by subtracting the product of the parallelogram’s area and Xcg^2. The Xcg is the horizontal distance from the parallelogram Cg to the external Y-axis from the inertia Iy for the parallelogram. The matching items are to be cleared.
The steps for calculating the inertia Iy for the parallelogram at the Cg are shown in detail on the next slide.
The final expression for the moment of inertia for the parallelogram about the Y-axis.
The value of the radius of gyration at the external Y-axis for the parallelogram can be obtained by dividing Iy by the area of the parallelogram. The expression for ry^2 for a parallelogram is shown in the next slide.
The value of the radius of gyration at the Cg for the parallelogram can be obtained by dividing Iy at the Cg by the area of the parallelogram. The expression for rg^2 for a parallelogram is shown in the next slide.
The slide image shows the moment of inertia, Iy, for the parallelogram at the Y-axis, the radius of gyration, and matches the previous calculation as shown in this post.
This is the end of our post for the Moment of inertia Iy for the parallelogram.
You can download and review the content of this post through the following pdf file.
This is the next post, Iy for the trapezium.
For the use of a calculator for various shapes, please find the Moments of Inertia – Reference Table.