4-Moment of inertia Iy for the rectangular section

Moment Of Inertia Iy for a rectangular section.

Moment Of Inertia Iy for a rectangular section-video.

Since we have estimated the moment of inertia about the X in the last lecture for the rectangular section. we will be able to estimate the radius of gyration.

By saying that, Kx=sqrt of Ix /A. our A=b*h for the rectangle, where b is the breadth, height, and the moment of inertia about the CG is b*h^3/12. So Kx = We open one bracket. We are writing (b*h^3/12), all divided by b*h, which is the area inside the bracket raised to the power of 1/2.b will go with b, and h will go with h.
So we are left with h^2/12, Raised to the power of 1/2, for Which kxg = h/2 *SQRT of 3.
While for the kx for the external axis at the left corner will be kx= h/SQRT of 3. This is a part of the video, which has a closed caption in English.

if you wish to watch the video on U-tube, here is the link.

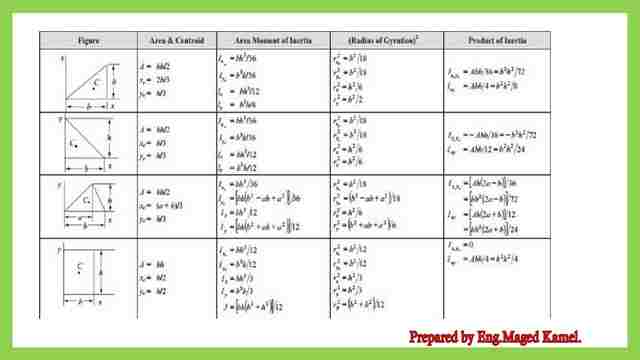
FE  reference manual tables for the area and moment of inertia for the Rectangular section.

The first four items quoted from the NCEEs reference manual 9.5, are for the shapes of a right-angle triangle, represented by two cases, a triangle shape, and the last case is for a rectangle.

How to get kx the radius of gyration for the rectangular section at x?

1-If we want to get k^2x at the external axis passing by the base, we will divide the
Ix value which is( b*h^3/3/Area), then we will getk^2x=h^2/3.  2- But if we want to get k^2x at the axis passing by the center of gravity, by the base, we will divide Ixg value which is (b*h^3/12/Area), then we will get k^2xg=h^2/12.      

How to get the moment of inertia Iy for the rectangular section?

A- using a vertical strip.

The next step is how to estimate the moment of inertia About y. The moment of inertia Iy for the rectangular section at the y-axis passes by the external axis at the left corner.

1-The strip area =dx*h, and the horizontal distance from the CG of that strip to the vertical axis y=x.
2-The moment of inertia for that strip =dIy=dA*x^2=h*dx*x^2.

3-The moment of inertia for the whole section is the integration of the strip from x=0 to x=b, where b is the width of the section, while b is the section breadth. 4-The moment of inertia Iy for the rectangular section is =h*b^3/3 about the external axis-Y.

5-Iyg is the moment of inertia at the CG -hb^3/12, from the parallel axes theorem Iyg=Iy-(Area(x cg)^2=hb^3/3-(bhb^2/4)=bh^3/12. as shown in the next image.

A- using an infinitesimal area (dx*dy) .

The moment of inertia About y. For the moment of inertia, for the rectangular section at the y-axis passing by the external axis at the left corner, by using the infinitesimal area (dx*dy), we will use a double integration method.

1-The strip area =dx*dy, and the horizontal distance from the CG of that strip to the vertical axis- y=x.
2-The moment of inertia for that strip =dIy=dA*x^2=dy*dx*x^2.
3-first we integrate from 0 to h for dy, then we integrate from x=0 to x=h.
4-The moment of inertia Iy for the rectangular section is =h*b^3/3 about the external axis-Y.
5-Iyg is the moment of inertia at the CG -hb^3/12, from the parallel axes theorem Iyg=Iy-(Area(x -cg)^2=hb^3/3-(bh)b^2/4)=bh^3/12. as shown in the next image.

The first method to estimate Iy for the rectangular section at the Cg.

1-Estimate the Iy about the external axis y which passes through the outer side of the rectangle, we have already estimated it as (h*b^3/3).

Iyg can be obtained by using the parallel axes theorem.

Another alternative method or direct method for Iy for the rectangular section at CG.

There is another method to get the moment of inertia Iyg directly about the axis y’ passing by the Cg by producing a strip of (dx*h), the distance to y’ axis=x. The inertia of the CG is the integration of that strip, but from x=-b/2 to x=b/2.
Iyg is Iy for the rectangular section at the CG will be h*b^3/12 the same as the value obtained from the previous calculation.

The radius of gyration Ky & kyg for the rectangular section.

Ky =sqrt of Iy / A, where Iy is Iy for the rectangular section since Iy=(bh^3/3) and A=bh, as the numerator all under the sqrt, so this h will go with h, one b goes with one b, we are left with Sqrt(h^2 /3).

K^2gy =IyG / A Iyg=bh^3/12 and A=bh, as the numerator is all under the sqrt, so this h will go with h, one b goes with one b, we are left with Sqrt (b^2 /12).

This is the PDF used for the illustration of this post.

For an external resource, Engineering core courses, the moment of inertia.
The next post: How to get the product of inertia for a rectangle? this is a link, Product of inertia Ixy- for the rectangular section.