11-Moment of inertia Iy-Case-2 for a right-angle triangle.

Moment of inertia Iy-Case-2 for a right-angle triangle.

Case of Moment of inertia Iy-case-2-for y-axis at the left side.

There are two conditions for the y-axis, the first is when the y-axis passes by the intersection point between the base and the hypotenuse or the left corner.
1-For Iy estimation,  for case -2, a vertical strip will be used, the strip width is dx and its height is y.            
  2- Since the strip height starts from the base and intersects with line  AC, the y value is the same as the line AC equation, that is y=h*x/b, for the x value it will be=b*y/h.  
3- The moment of Inertia due to that strip about the Y-axis is equal to A*(x^2).

4- Integrate from x=0 to x=b. Iy=(h*b^3)/4 is the final solution. This is a right-angle triangle’s Inertia Iy-case-2.

   
The radius of gyration Ky for right-angle. 

   5- from the expression that Ky=sqrt(Iy/A), we can get the radius of gyration about the y-axis, since A=(1/2)b*h. The value of the moment of inertia, Iy=h*b^3/4. Then Ky=sqrt(h*b^3/4)/(1/2*b*h)= h/sqrt(2).                   

Moment of inertia Iy-Case-2 for right-angle, case of the Y axis is at the right side.

Let’s say we wish to move the Y-axis such that it, for instance, coincides with the triangle’s other side.
The y-axis coincides with the other side of the triangle, while the x-axis points left.
Once more, we’ll employ a vertical strip with height = y and width = dx.

1-For the estimation of Iy -case -2, a vertical strip will be used, the strip width is dx and its height is y.       
2- Since the strip height starts from the base and intersects with line  AC, the y value is the same as the line AC equation y=(h/b)*(b-x).
3-Moment of inertia due to that strip=dA*(x^2).
4- We will integrate from x=0 to x=b, the details of integration are shown in the next slide. The final answer is Iy=h*b^3/12.    
When comparing this value with the previous value for Iy when the y-axis is at the left, we find that the Iy value becomes smaller, and the radius of gyration Ky for right-angle case-2 when the y-axis is on the right side.   

5- from the expression that Ky=sqrt(Iy/A), we can get the radius of gyration about the y-axis, since A=(1/2)b*h.
Iy=h*b^3/12. Then Ky=sqrt(h*b^3/12)/(1/2*b*h)= h/sqrt(6).      

Inertia Iy-at the CG for a right-angle triangle.

1-For Iyg estimation, we will deduct the product of A*x_bar^2, from the Iy-inertia-case-2-Iy value which is =h*b^3/4.
 2-We get the value of Iyg=h*b^3/36, which was derived from the case where the y-axis is located on the left side, I call it Y1 as shown in the slide.

3- The moment of inertia about the CG-Iyg value for the second case, where the y-axis is located on the right side, is the same value after subtracting Ax bar^2 from Iy value =hb^3/12 for the expression of Iy.

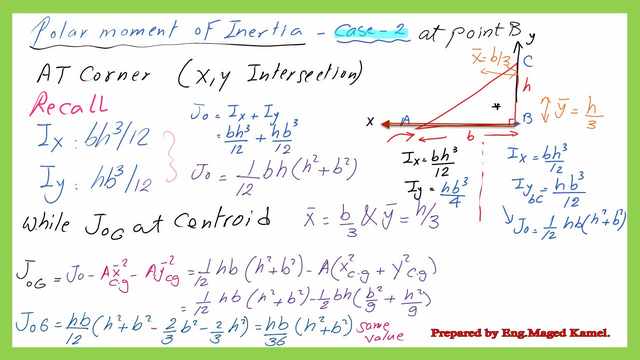
Polar Moment of inertia Jo for right-angle for y-axis at the left side.

The polar moment of inertia Jo for right-angle case-2 for the y-axis at the left side can be estimated by adding the sum of Ix and Iy. We have Ix value =bh^3/12, while Iy=hb^3/4 when the y-axis is at the left. That position will be called Y1.
Jo=(bh^3/12)+(hb^3/4).

The final value for J0G, which is the polar moment of inertia at the Cg can be written as The steps to get the polar moment of inertia at the CG.

The Polar moment of inertia Jo for right-angle case-2 for the y-axis at the right side.

The polar moment of inertia jo can be estimated by adding the sum of Ix and Iy. We have Ix value =bh^3/12, while Iy=hb^3/12 when the y-axis is located at the right that position will be called Y. Jo=(bh^3/12)+(hb^3/12).

To get the value of the polar moment of inertia for the right-angle triangle. at the CG, deduct Ax^2 plus Ay^2cg from Jo, we have Xcg equals b/3, while ycg=h/3. Jocg=1/12*h*b*(h^2+b^2)-1/2*(bh)*(x^2cg+ycg^2). the final value of jcg=1/36*(h*b)(b^2+h^). the result matches with the previous estimated value of Jcg while considering the x and y axes at the left corner.

This is the table for the plain shape areas and their inertia values.

This is the PDF file used in the illustration of this post.

For an external resource, the definition of the moment of inertia with solved problems, is for the 2nd moment of inertia.

This is a link to my 1-Moment of Inertia- English – YouTube on YouTube.
This is the next post, Product of inertia Ixy– for the right-angle triangle-case-2.