Polar Moment Of Inertia J- For the Triangle.
Our aim is to get the J for the triangle at point a, where the two axes x and y intersect. we consider the triangle as composed of two right-angle triangles. One right angle with a base equals (b-a), while the other right angle with a base equals a.
The Ix value can be obtained by adding Ix1 plus Ix2. The Ix1 equals a*h^3/12. For the other right angle triangle case 1, Ix equals (b-a)*h^3/12. the final ix value can be written as equal to h^3*b/12. please refer to the next slide image for more details. For more details about the moment of inertia at the x-axis for the triangle refer to the Moment of inertia Ix- for a given triangle. Please refer to post 13.
We will add both Ix+Iy as follows: first the moment of inertia Ix at point a equals (b*h^3)/12.
While the value of Iy=(b*h)*(a^2+b^2+ab)/12. For more details about the moment of inertia at the y-axis, the triangle refers to the post 14-moment of inertia Iy– for a given triangle.
The moment of inertia about y, Iy at point a can be obtained by adding the inertia as Iy for the two right-angle triangles.
Iy value equals b*h*(a^2+ab+b^2) this equation was derived in post 14.
Polar Moment Of Inertia J- For the Triangle at the left corner point.
Add the Ix +Iy to get the final value for the polar moment of inertia for the triangle at the left corner point a.
3-:J at point, a, after adding Ix+Iy.This is the final value of the polar moment of inertia for the triangle at edge point a as shown in the next slide image. j0=h*b/12*(h^2+a^2+ab+b^2).
Polar moment of inertia J for The triangle at the CG.
.There are two ways to get the expression for Jg, the first way is to deduct the product of A*(xbar^2+y bar^2) from the J value. where x bar is the horizontal distance from the CG of the triangle to the vertical axis y at point a. Y bar is the vertical distance from the CG of the triangle to the horizontal axis -x axis y passing by the point a. For more details on how to find the x-bar.
For more details on how to find the y-bar, please refer to post 13 Moment of inertia Ix- for a given triangle. The calculation for the polar moment of inertia at the centroid. of the triangle.
This is the final expression for j at the Cg. Jg=h*b/36*(h^2+a^2-ab+b^2).
The second method is to get the Polar moment of inertia J for the triangle at the CG.
The second method to get the polar of inertia is to add the value of the moment of inertia Ix gat the center of gravity CG value to the value of the moment of inertia at the y-axis passing by Tthe CG, Iyg at the Cg or the sum of Ixg+Iyg for the triangle. The Ixg at the Cg will be equal to b*h^3/36. The Iyg for the triangle will be equal to b*h/36*(b^2+a^2-ab).
Both ways will lead to the same result.
This is the list of inertia for triangular shapes quoted from the NCEES tables of inertia. there are other shapes for instance a right angle triangleas case 1 and case 2 and also a rectangle.
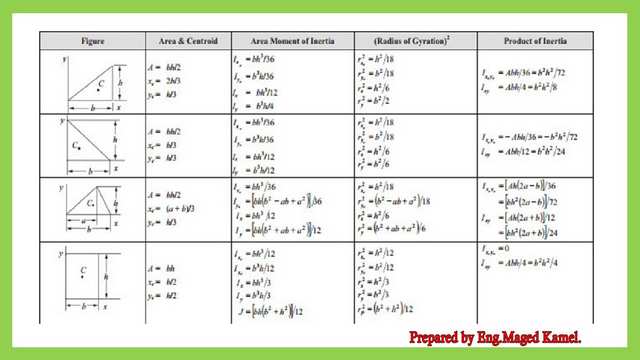

This is the pdf file used in the illustration of this post.
For an external resource, the definition of the moment of inertia with solved problems for the 2nd moment of inertia.
This is the next post moment of inertia for an isosceles triangle-Ix, Iy.

