Last Updated on March 6, 2024 by Maged kamel

Moment of inertia Ix-for a triangle.

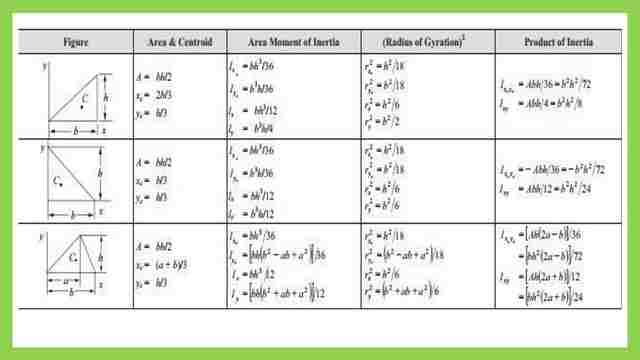
List of the area moment of inertia for a triangle.

The value of the area and Moment of inertia for the triangle is the third item in the shown table from the NCEES reference handbook-3.50. the shown table lists the values of Ix and Iy for the triangle.

Step-by-step guide for the calculation of Ix-for a triangle.

1-For the moment of inertia  Ix estimation for a triangle, we will consider that triangle, as composed of two right-angle triangles, for the first right-angle triangle, will be considered as case No.2. Please refer to the previous posts for the complete estimation for the values of inertias. For case, number #2, the y-axis is passing by the left corner a.

Case -2 right angle triangle, which is the first right-angle triangle has a base =a and a height equals h as shown in the next slide image.

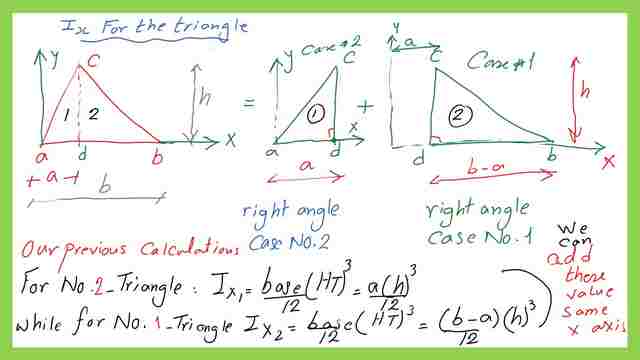
While another right-angle triangle, will be considered as case no.1, it has a base equal (b-a) and a height equal h . We will list the values of inertia as Ix1 and Ix2. Ix1 is the inertia at x-axis for case No.2 , while Ix2 is the value of the moment of inertia for the case No.1 triangle.

2-For Ix estimation adding the two values of inertia (a)*h^3/12+(b-a)*h^3/12 will give us 

3-For the k^2x value, we will divide the Ix value /area of the triangle, so we get y bar value for the triangle will be found as equal to h/3.

4- For the moment of inertia Ixg at the CG, we are going to estimate the y-bar for the triangles shown in the next slide from the first-moment area.

5- Ixg=Ix-A*y bar^2, after substitution we will get the moment of inertia Ix for a triangle at the Cg as :

6-The radius of the gyration of the triangle can be estimated from the following relation. The square value of the radius of gyration for a triangle at the Cg can be found to be equal to h^2/18.

This is the pdf file used in the illustration of this post.

For an external resource, the definition of the moment of inertia with solved problems, is the 2nd moment of inertia.

This is the next post, Moment of inertia Iy– for the triangle.