Solved Problem 4-5-How To Design A Steel Beam?
A Solved problem 4-5.
A solved problem 4-5 from Prof. Alan Williams‘s Structural Engineering Reference Manual.
Design of beam according to LRFD for part a.
Part A includes the lightest adequate W section for design. We have to identify which region That w section is located according to bracing. This is a design problem for which, the distance between bracing for a beam is Lb < Lp. After the design, we will get the Lb value from the next step 3.
For the LRFD design:
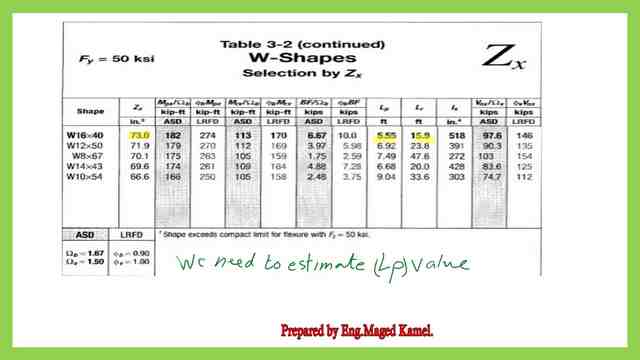
1-Estimate the preliminary Zx value by considering that φbMn=Mult, since Mn=ZxFy.


We can get the plastic section modulus Zx= Mult /(φb*Fy). We go to Table 3-2, where sections are sorted by Zx, and select the first bold section with Zx selected > Zx estimated.
2- From table 3-2, we get the section W16x 40, which has Zx =73.0 inch3 >72.0 inch3, which is the preliminary value for Zx.
We can get the bracing length required from Table 3-2 at the plastic stage Lp and lr value.

This is a reminder of the Graph of Mn the bracing distance and the different zones.


If we wish to check the Lp value. Lp can be estimated from the relevant formula Lp=ry* (300/sqrt(Fy)), but we need to have ry value.
3- From table 1-1 get the Sx value, ry for the selected section, and apply the equation of LP=ry*300/sqrt( Fy) or from table 3-2 for Fy is equal to 50 ksi.
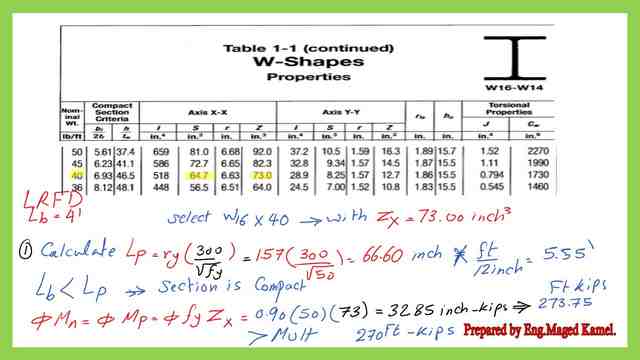

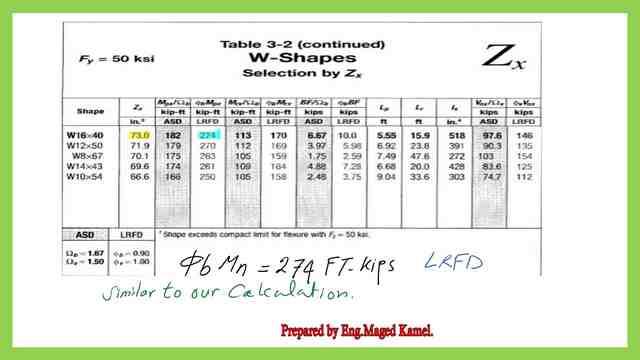
4- Since the given bracing length Lb is smaller than Lp, the section is compact, φb*Mn= φb*Zx*Fy, to be divided by 12 to get the value in Ft-kips-LRFD. we get the φb*Mn=274 ft. kips. The same value φb*Mn can be obtained from Table 3-2, as seen in the next slide.

Design of beam according to ASD for part a.
The ASD calculation is shown in the next slide, here are the following steps to implement:
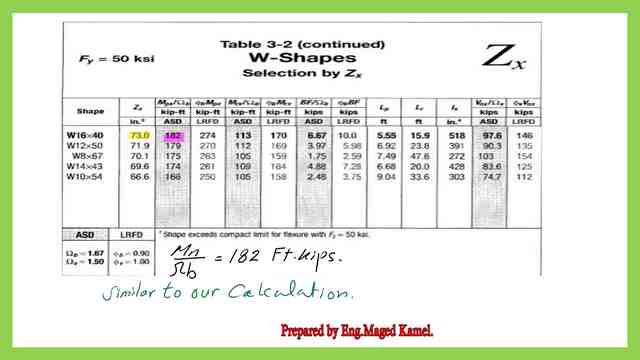
1-Get a preliminary Zx value by considering that (1//Ω)*Mn=Mtotal, since Mn=Zx*Fy.
We can get Zx= Mtotal /(1/Ω)*Fy). 2-From table 3-2, select the lightest w section, that gives Zx>Zx preliminary.
The selected W section is W16x40, Zx of the selected section=73.00 inch3, which is >72.144 inch3 as per requirement.
2- From table 3-2, we get the section W16x 40 that has Zx =73.0 inch3 >72.0 inch3, the preliminary value for Zx.
We can get the bracing length required from table 3-2 at the plastic stage Lp. Lp can be estimated from the relevant formula Lp=ry* (300/sqrt(Fy)), but we need to have ry value.
3- From table 1-1 get the Sx value, ry for the selected section, and apply the equation of LP=ry*300/sqrt(Fy), or from table 3-2.


4- Since the given bracing length Lb is smaller than Lp, the section is compact, (1/ Ω)*Mn = (1/ Ω)*Zx*Fy, to be divided by 12 to get the value in Ft-kips-ASD.
5- Check that the estimate (1/ Ω)*Mn is >=total moment Mt.
The same value (1/ Ω)*Mn can be obtained from Table 3-2, as we can see from the next slide.

Design of beam according to LRFD for part b.
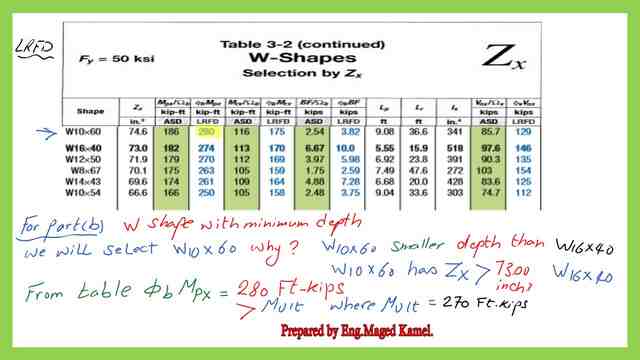
This is part b, determine the W shape with minimum allowable depth, as per LRFD.
The selection is based on the minimum depth.
We will select W10x60 since the depth is smaller < depth of W 16×40 as shown in the next slide, then check that the φb*Mn> Mult.

Design of beam according to ASD for part b.
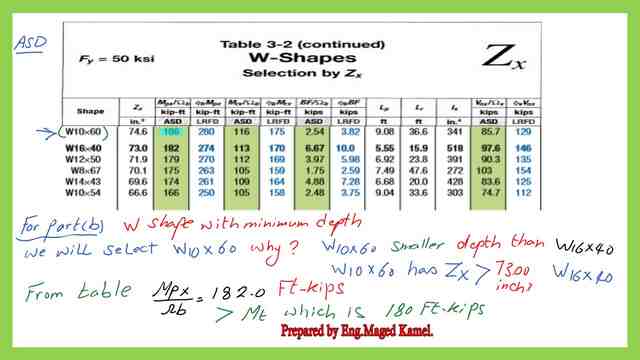
This is part b, W shape with minimum allowable depth, as per ASD, for the selection based on the minimum depth.
We will select W10x60 since the depth is smaller < depth of W 16×40 as shown in the next slide, then check that the (1/ Ω)*Mn > Mt.

This is the pdf file used for the illustration of this post.
For a useful external source, please follow this link– lateral Torsional Buckling Limit State.
For the next post, review the Information of Lp, Lr. This post is an introduction to the different terms of the Lp and Lr for a steel beam.

