Last Updated on February 29, 2024 by Maged kamel

Moment Of Inertia Ix for the rectangular section.

The objective of the lecture includes 5 points. The next image explains the first three objectives as follows.

The next image explains the other two objectives as follows.

 The procedure to get Ix for the rectangular section.

1-Consider a horizontal strip of breadth=b, and thickness of dy.
2- The vertical distance of this strip from the external axis X passing by the left edge corner is y.

3-The expression of the Moment of inertia for that strip is dIx =bdyy.

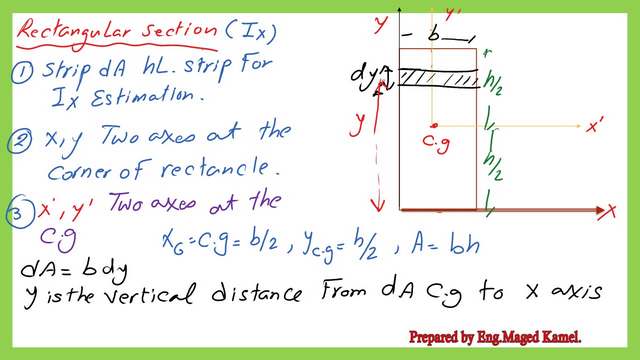
4-Ix value, by integrating from y=0 to y=h, Ix=∫ dIx=∫b*y*dy=b*y^2 from y=h to y=0, the integration will be Ix=b*h^3/3, this is the moment of inertia about ann external axis passing by the left bottom corner of the rectangle.

Moment of inertia Ix for the rectangular section at the CG-Ixg.

5- For the Ix_g , the moment of inertia about the Cg, we will use the parallel axes theorem and deduct the (area*(h/2)^2), so we can get the values as shown attached.

6- We have already estimated ix about the external axis as Ix=b*h^3/3, we will deduct(b*h)*(h/2)^2=b*h^3*(1/2-h^2)/(4)=b*h^3*(2-1)/4=b*h^3/12 which is the value of Ixg, which is the moment of inertia at the CG of the rectangular section of dimension (b*h).

Another alternative method for Ix for the rectangular section about the Cg.

We can get the expression of the moment of inertia about the CG directly by integrating the strip of area (b*dx) from y=-h/2 to y=+h/2, Ix=∫ b*dy*y^2=(b*y^3/3), we will substitute for y=h/2 and y=-h/2.

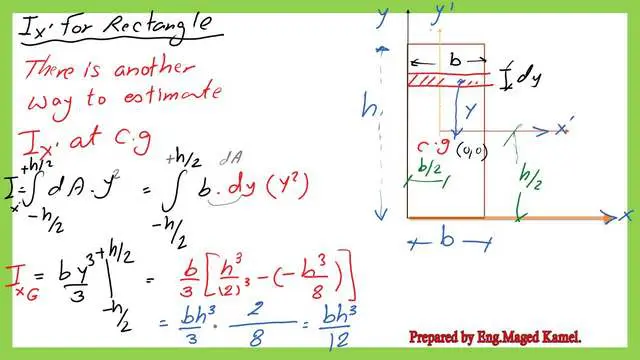
Ix=(b*(h/2)^3/3-b*(-h/2)^3e =(b/3)*(1/8)*(h^3+h^3)=2*b*h^3/24=b*h^3/12.
As we can see in the next slide, both two expressions are identical whether using the parallel theorem or the direct integration about an internal axis x’.

The radii of gyration for the rectangle section.

The radius of gyration can be estimated by considering that K^2x=Ix/A, where k^2x is the square of the radius of gyration about the x-axis, So Kx=sqrt(Ix/A). for tx=b*h^3/3, the area is(b*h) then we can get the expression for K_x as follows:

The radius of gyration at the CG can be estimated by considering that K^2xg=Ixg/A, where k^2xg is the square of the radius of gyration about the X’-axis.

For Ix=b*h^3/12, the area is(b*h) then we can get the expression for K_xg as follows:

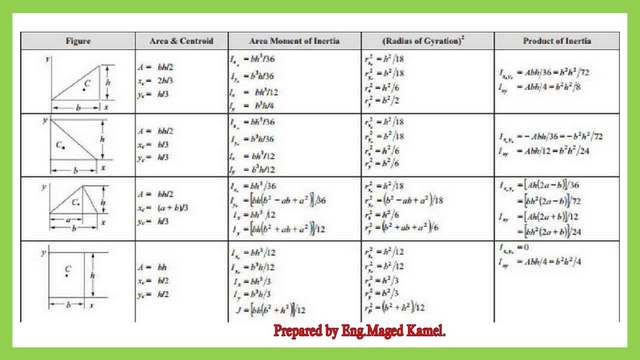
The list of the values for inertia for plain shapes.

The shown table is a list of inertia for plain sections. The case of the inertia of the rectangle is shown as the fourth item.

This is the PDF used for the illustration of this post.

This is a link for a good external resource, to serve as a calculator, Calcresource.
Next post: the moment of inertia Iy for the rectangular section.