5b-Find the three unknowns for Second solved problem

Last Updated on December 17, 2025 by Maged kamel

Find the three unknowns for the Second solved problem.

This is the video that illustrates the content of this post.

What are the two methods used to solve for the three unknowns?

There are two methods to find the three unknowns x1,x2, and x3. The first method is to consider A*x = b and let A = L*U. The matrix A can be rewritten as L*U. The product of A by x can be written as L*U*X=B. Introduce a matrix C as C*X=B and the L*c=b. Solve for the value of C by multiplying L-1*L*C=L-1b and nd later solve for the inverse of the upper matrix—finally, x=U-1*B.

The second method is to get L and U values, find the inverses of both L and U, and then multiply U-1*L-1*L*U*X. The product of these matrices leads to I*x= U-1*L-1*B. Hence, we can get the values of the three unknowns. Please refer to the following slide image for more details.

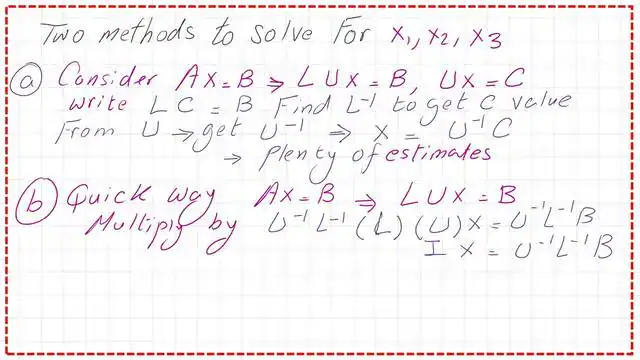
To find the inverse of a matrix, we use its minors and cofactors. The following slide shows the data for minors and cofactors.

What are the minors and Cofactors values for the lower matrix L?

We have estimated the L matrix from the previous post; we need to find its inverse. We need to find the cofactors for the first row (C11, C12, C13) and the cofactors for the second row. c21, C22, and C23. The following slide shows how to estimate the Cofactors and their values from the matrix L.

The cofactors C31, C32, and C33 for the L matrix.

The values for the cofactors C31, C32, and C33 for matrix L are shown in the following slide image. To get the cofactor values in the column-wise form for the inverse, we need the determinant of Matrix L. The determinant value equals 1, all diagonal values are 1 for the L matrix.

Get the inverse matrix L-1 and matrix C.

For the second solved problem, LU decomposition, we need to estimate the inverse matrix of L, which is the Cofactor matrix divided by 1. The inverse matrix of L is( 1, 0, 0, -3,1, 0, 1-, -1,1). We use the expression L*C = B. We multiply both sides by L-1; we get C = (L-1)* B. The value of C is (3, 4, -6), which is a (3×1) matrix. Please refer to the following slide image for more details. But U*X=c. We need to estimate the inverse of the matrix U to get the column vector X.

What are the minors and Cofactors values for the upper matrix U?

We have estimated the U matrix from the previous post; we need to find its inverse. We need to find the cofactors for the first row (C11, C12, C13) .The adjugate of the upper Matrix is the cofactor transpose. The cofactor C11 is equal to +6; the cofactor C12 is equal to 0. The cofactor C13 is equal to 0.

The following slide shows the cofactor values for the second row. C21, C22, and C23 of matrix U.The adjugate of the upper Matrix is the cofactor transpose. The cofactor C21 is equal to -6, the cofactor C22 is equal to +3; the cofactor C23 is equal to 0.

The cofactor C31 is equal to -4; the cofactor C32 is equal to -2. The cofactor C33 equals +2.

The determinant value of the Upper matrix is equal to +6.

The inverse of Matrix U is a 3×3 matrix with the first Row as (6, -6, 4, 0, 3, 2, 0, 0, 2), all divided by 6. 

Get the inverse matrix U-1.

For the second solved problem, LU decomposition, the product of the inverse of U and C equals the column vector X. X1 = 3, X2 = 4, X3 = -2.

It is essential to check that the values of the three unknowns are correct; we double-check by multiplying A by x and verifying that the product equals vector b, which is valid.

As shown in the next slide, we can obtain the values of the X column vector by multiplying U-1*L-1*b to get x1, x2, and x3.

This is the PDF file for the second part.

The following post: 5c- Solved problem for x-y-z values by LU decomposition.

HELM-Helping Engineers Learn Mathematics.

This is the Omni calculator for estimating various linear algebra items – LU Decomposition Calculator.

This is a link to another Calculator for matrices.