Last Updated on July 23, 2025 by Maged kamel
Solved Problem 5-10: Available strength for short column-slender W section.
We are going to see the solved problem- 5-10. From the unified design of steel structure, for local buckling, our steel section for the column is a W16x26 section. Kl at y direction =5.00 ft. The solution is based on CM#14, AISC-360-10.
It is required to estimate the available strength of that column. The column is slender, as shown in the following picture, after verifying the Flange and web local buckling parameters.
This is the table of shapes and corresponding Fy, Fult values.

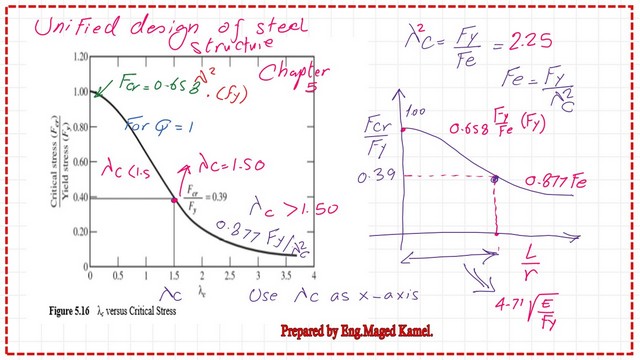
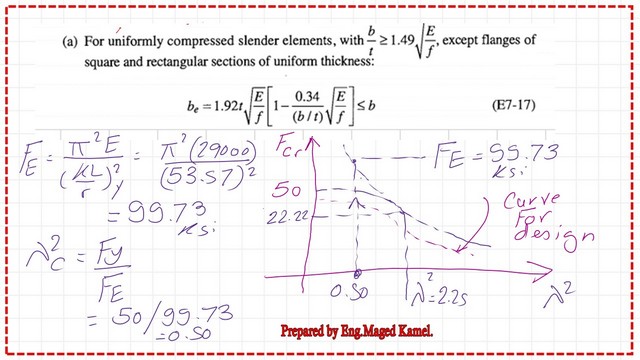
This is the λ2 expression used for earlier versions, for which λ2=Fy/Fe, where Fy= yield stress of the section, Fe is the Euler stress, and for the general buckling equation, the Fcr equations are adjusted accordingly.

A solved example 5-10 for the available strength.
This is a newly solved problem 5-10 from the unified design of steel structures by Louis F. Geshwendener, it is required to determine the available strength of a compression member with a slender web, the section is W16x26 as a column with lcy =5.0 ft.
Step-1- Check whether the column is long or short, by using the limiting ( kL/r) value for the solved problem 5-10, estimated from the formula (KL/r)=4.71sqrt(e/FY)=4.70SQRT(29000/50)=113.43.

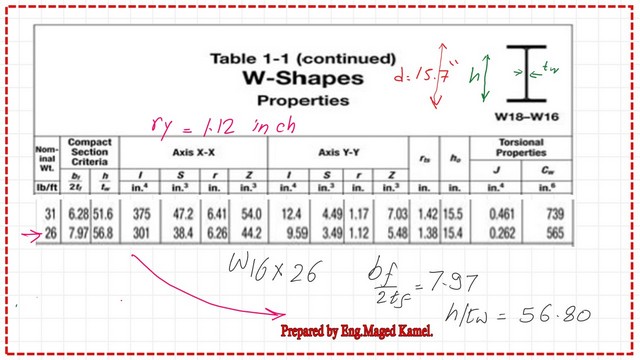
Step-2-Get the Area of the section, ry radius of gyration about y, for the solved problem 5-10.
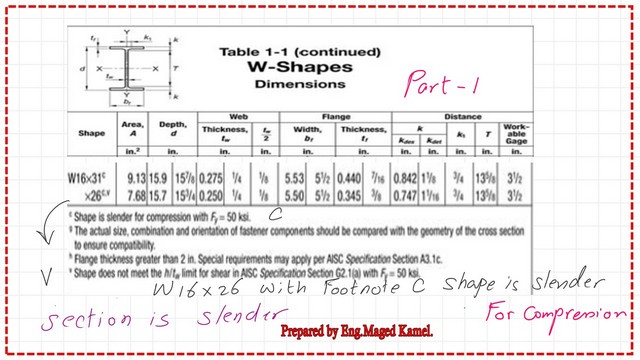
From the relevant table of W16x26, we get the data for the area, try,d, h, t-web, and the (K*l/r) at the y-direction (1*5*12/1.12)=53.57, which is < 113.43; then the column is short.
The data can be found in Table 1-1 for the corresponding section. Bf, tf, h, t web, section W 16×26 has a footnote c, which means that it does not meet the requirement of h/tw.
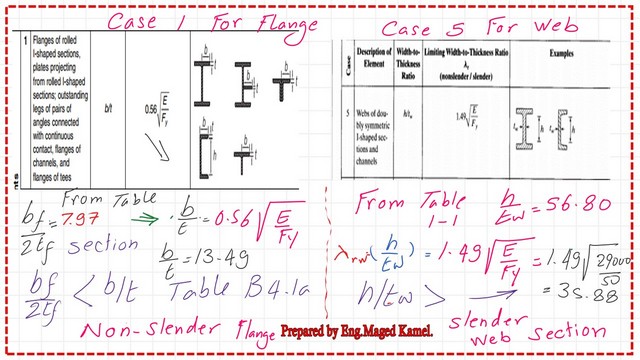
Step-3- Check the column, whether elastic or inelastic column, for both flange and web. From the following image, we get the values of Bf/2tf=7.97 &h/tw=56.80.
Is a column elastic or inelastic?
We will check against the value of 0.56*sqrt(E/fy), which yields 13.49 > bf/2tf for the flange in problem 5-10.
While the value for W16x26(hw/tw) = 56.80 is given in the table, the limiting value is 1.49*sqrt(E/fy), which yields 33.72. This value is less than 56.80, so the section is a slender-web section.
Fcr value for the column.
Step 4: Estimate λ2, which is Fy/FE, and obtain the relevant Fcr. Consider Q=1, where Q is the reduction factor, Fe value=99.73 ksi, while Fy=50 ksi.
λ2=(50/99.73)=0.50, we will evaluate Fcr by using the equation fcr=0.658^(λ2Q)(Q*Fy).
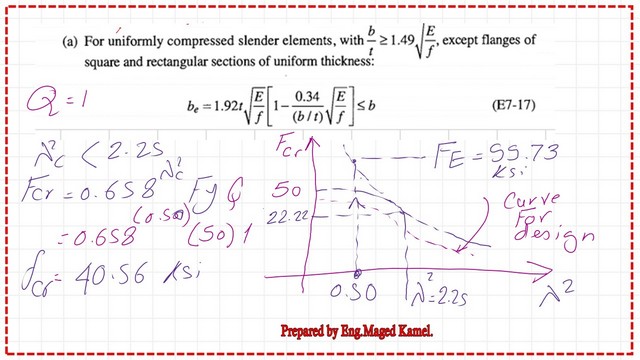
We will evaluate the critical stress Fcr by using the equation Fcr=0.658^(λ^2*Q)(Q*Fy)=0.658^(0.50)*50=40.56 ksi.
The value of the effective area.
Step-5 We will estimate the value of he from the E-7-17. According to the AISC equation E7-17, we have Fcr = f = 40.50 ksi. the value of b/t=h/tw=56.80. We check that he is <h web; the value obtained=10.80″<14.206″.

Step 6: We will estimate the value of A eff after deducting the ineffective area. The effective area A eff is obtained from Agross- Aw+(he*tw)=7.68-3.55+2.7=6.83 inch2.

Estimate the available strength for LRFD and ASD designs.
Step-7 Use the value of A eff and the Fcr to get the LRFD and ASD values. We have an area of 6.83 inches², while the stress is 40.50 ksi.
Estimate the Strength value for the column as LRFD value =Φc*Pn=Φc*For*A=0.90*40.50*6.83=250.0 kips. For the ASD value, Aeff*Fcr/Ω = 7.68*40.50/1.67 = 166.0 kips, which was the final result for problem 5-10, without using more iterations, considering Q = 1.0.

This is the link to the next post is Solved Problem 5-10 with more iterations.
This is a link to A very useful external link Chapter 7 – Concentrically Loaded Compression Members.