Last Updated on January 15, 2026 by Maged kamel
Newton-Raphson method.
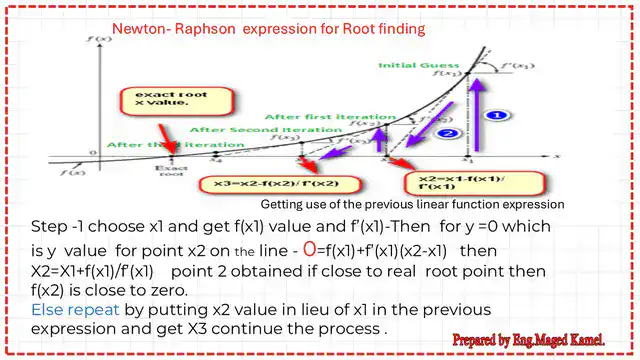
Newton-Raphson’s method is another root-finding method. The Newton-Raphson expression of root-finding utilises the linear approximation, which we have discussed.
From the next slide image. L(xb)=f(xa)+f'(xa)*(xb-xa) as a is the starting point and xb is the ending point.
Now, if we consider that L(xb) approximately equals (xb), and create a little modification to the previous equation by letting (xb-xa) on the left side, and then rewrite the equation.
We could say x final=x intial+(1/ slope at the ix initial)+(1/ slope at x intial)*(f(x final)l- f(x initial).
If we are looking for xb where the root =0, or saying f(xb)=0.
The formula will be xb=xa+(1/f'(xa)(0-f(xa)=xa-(1/f'(xa)(f(xa).
The formula can be used to obtain the distance x to the root point b we are looking for.

This will create another form of the equation as (xb-xa)=(1/f'(xa))*(f(xb)-f(xa). The next step is to find the value of xb, which is=xa+(1/f'(xa))*(f(xb)-f(xa).
Suppose we have a curve and are looking for its root at a given point. We want to find the x-value of that root point. So we say that if we have a point x1, we go up, then make a tangent to the curve at that point.
So we get another point, x2, and a relation between x2 and the old point. This relation will be x2=x1– f(x1) /f'(x1) as shown in the next slide image to continue this process till a point where we have f(x) close to or =0. This is the Newton-Raphson method.
A solved problem using the Newton-Raphson method.
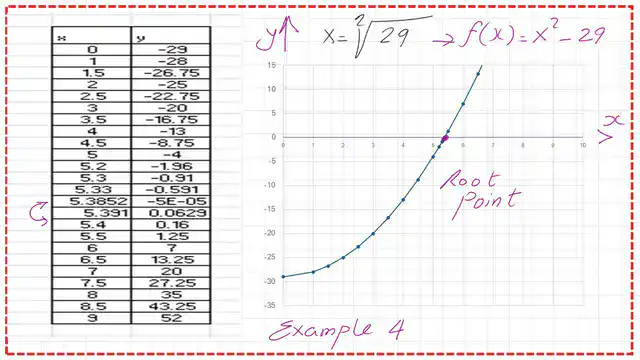
First, the Newton-Raphson equation is written. followed by a solved example #4. Use the Newton method to find the roots of the √29. The solution will be made through the next steps.
We put x= √ 29, or it could be expressed as X^2= to 29, then let X^2-29 =0.
1-We readjust the formula for the function, and we equate it to 0. The f(x) is to be written as f(x)=x^2-29.

We use an Excel graph for the given function to locate the point where f(x)=0, which is between 5.3852 and 5.391.
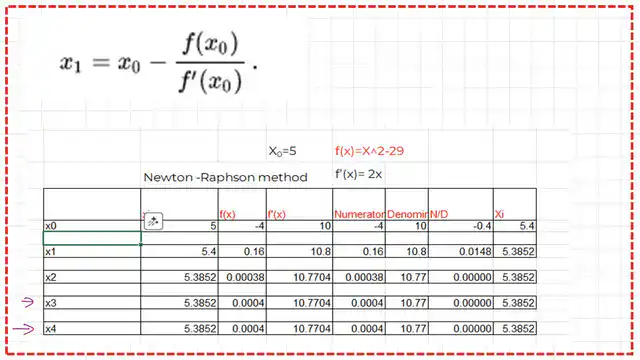
2-We put x0=5 as starting point after that get f(5) = 5^2-29=-4.
The negative sign will change the relationship, as we will see later.
3-Estimate the f'(x0=5) =(2*x0)-0=2*5.0=10.00.
4- Estimate X1 value by using the Newton-Raphson method, X1=5-(-4/10.00)=5.40.
5-This is for the first iteration. We started from X0, got X1, then again substituted with this new value, which we are getting: 5.40.
For the second iteration.
6- We put x1=5.40 as obtained from the previous iteration, f(5.40) = (5.40)^2-29=+0.16.
7-Estimate the f'(x1=5.40) =(2*x1)-0=2*5.40=10.80.

8- Estimate X2 value by using the Newton-Raphson method, X2=5.40-(+0.16/10.80)=5.3852.
9-x2=5.3852, check (5.385)^2-29=-0.001775 not zero, so proceed to get the next point x3.
For the third iteration.
10- We put x2=5.3852 as obtained from the previous iteration, f(5.3852) = (5.3852)^2-29=–0.000379
11-Estimate the f'(x1=5.3852) =(2*x2)-0=2*5.3852=10.7704.
12- Estimate X3 value by using the Newton-Raphson method, X2=5.3852-(-0.00022/10.7704)=5.38516.
13- The value of x3, x3=5.3852, check (5.38516)^2-29=4.2E-10 close to zero.

This is the Excel sheet showing the iterations of the different f(x) values and their first derivatives.
The PDF file for this post and the following post can be reviewed and downloaded via the following document.
This is a useful link for a numerical analysis calculator.
The next post is about the solved problems for the Newton-Raphson method.