Last Updated on March 21, 2024 by Maged kamel
Solved problems for Newton-Raphson method.
The first problem of the two Solved problems for Newton-Raphson method
Another solved problem for the Newton-Raphson method for root extraction: find the roots of x^3-3x-5=0.
1- starting by the initial point x0=3.00.
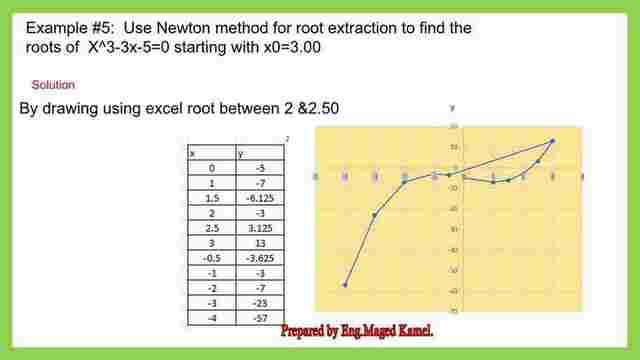
First, we try to find that root value by plotting the curve by plugging different values of x for example starting from 0 to 3.0 and negative values from x= -0.50 to -4.00.
We are getting the corresponding values of y accordingly, to find roots, we find that the function value between one positive and one negative review lies between x=2 and x =2.50.
1-So our first iteration is selecting x0 value =3.
2-Get f(x0=3) and f'(x0=3) f (x) is =x^3-3x-5=0 and f'(x) = 3*x^2-3.
At x0=3 then f(3) = 3^3-3*3-5 =13 and f'(x0=3.00)=3*(3)^2-3=24.00.
3- X1 =3-(13/24)=2.45833.

For the second iteration
4- Get the value of f(2.45833) and f'(2.45833), by using the excel sheet, we get a new value x2=2.2943 and the corresponding f(x) for each iteration, shown in the next slide.
We keep making iterations till we get x4=2.279, the error value is small.

The second solved Problem of the two Solved problems for the Newton-Raphson method
The second video includes an illustration of the second solved problem Number #6. This is the second solved problem of the two Solved problems for the Newton-Raphson method which is problem number 6: Use the Newton method for root extraction to find the roots of this function.
problem number 6: Use the Newton method for root extraction to find the roots of this function.
This is the first derivative of the function.
Solution: He did not give us a starting point so it is good to make a casing for the root range by substituting
1-We make the table we put different values of X and we find the corresponding values of our function. 2-We’ll find that when we plug X=0 then (0*e^0)-2, we get -2

3-For the next point where x=0.25, we get (-1.678994).
4-For x=0.50 we get -1.175639.
5- For x=0.750, we get. (-0.41225).
6- For x=1, we get +0.7182818.
So between x=0 and x=1.0 , x=0 is giving minus and x=1 is giving a positive value.
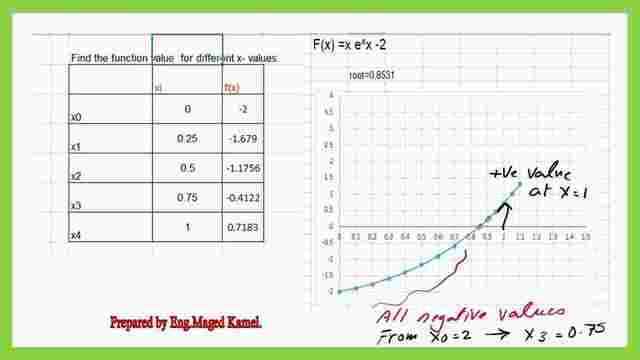
So our root should exist between 0 and 1. You have the choice either to start point x=0 or X =1. We put X=0 f(0)=(0)*e^0-2=-2.00, for the slope value, check the next relation, it will be=1.
x1=x0-f(x0)/f'(x0)=0-(-2/1)=+2.00.
For f(2), we have the value of 12.778, and f'(2)=22.16716. So X2 will be =+2-f(x1=2)/f'(x1=2).X2 will be =+2-(12.778/22.16716)=1.4325. After substitution, we get the value of the function as well as the derivative value. We use the expression of X3=x2- f(x2)/f'(x2), we get x3=1.034936.

It is better to calculate by using an Excel sheet this includes a starting point with a selected value followed by a column that represents the function value f(x) and another new column for the value of f'(x), a column for the numerator which I f(x), and the denominator which is ‘(x), then a column for numerator/ denominator.
We have two starting points the first starting point is x0=0, and the second starting point is x0=1. This is a function value f'(x) =4.34575 and we go on until we find that f(x) is coming closer to (0) at x value=0.8526.

When X =0.853003, the f(x) is zero if our starting point x0=1.

This is the pdf file used for the illustration of this post and the previous post.
The next post is about the Modified-Newton-Raphson method, for which there is a modification of the Newton-Raphson method.
This is a useful link for a numerical analysis calculator.

