Last Updated on December 10, 2025 by Maged kamel
We will introduce two practice problems for Ixy for trapezium, 8.43 and 8.49. These problems are quoted from Bedford and Fuksa’s Engineering Mechanics: Statics.
Two Practice problems for Ixy for a trapezium.
Two practice problems that illustrate how we can estimate the product of inertia about external axes as a first problem, while the second problem illustrates how we can get Ixy at the CG.
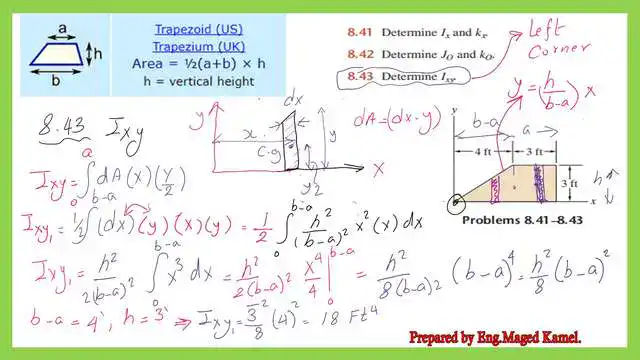
The first practice problem for inertia is No.8.43. Find Ixy for a given trapezium.
For the first of the two Practice problems for the product of inertia Ixy for a trapezium, we have a trapezium with a base length of 7 feet (b), an upper part length of 3 feet, and a height of 3 feet. It is required to determine the product of inertia Ixy about an external two axes at the left edge.
The first part is Ixy1, or the product of inertia for the triangular portion about the point of intersection of the two axes X and Y. We call it Ixy1. For a small strip dA, the value of this area is dx*y. The area dA creates dIxy about the point of intersection of axes X and y.
The product of inertia dIxy1=(dA*x*y/2)=(x*y^2*1/2*dx), but y has a relation of x as y=(h/(b-a)*x ,so the dIxy1can be rewritten as (h^2/(2*(b-a)^2)*(x^3*dx). We will integrate from 0 to (b-a) for the triangular portion.
finally the expression for Ixy1 can be written as (h^2*(b-a)^2/8). We can substitute h = 3Ft, a = 3 feet, and b = 7 feet. We can substitute these values in the Ixy1 expression. The Ixy1 value is equal to 18 Ft4. Please refer to the next slide image for more details.
Ixy2 product of inertia for a given trapezium by integration using a vertical strip.
The next step is to get the Ixy2 value for the rectangular portion. dIxy2 = (dx*h^2*x/2); we integrate from b-a to b, and the final value of Ixy2 is 74.25 Ft4. The final product of inertia Ixy for the given Trapezium will be equal to 92.25 Ft4.
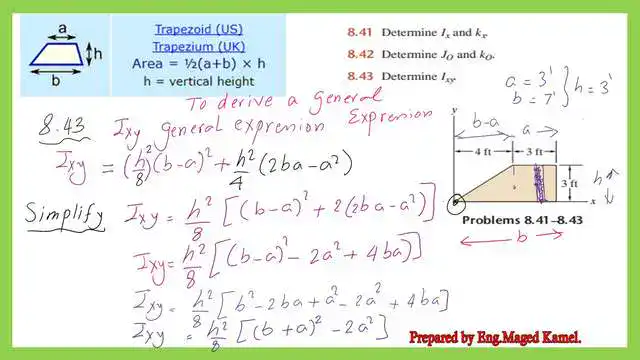
Derive a general expression for Ixy for a trapezium.
To derive an expression for Ixy for a trapezium, we add Ixy1 and Ixy2 and simplify the standard terms. For a more detailed illustration, please refer to the next slide, which shows the final Ixy expression.
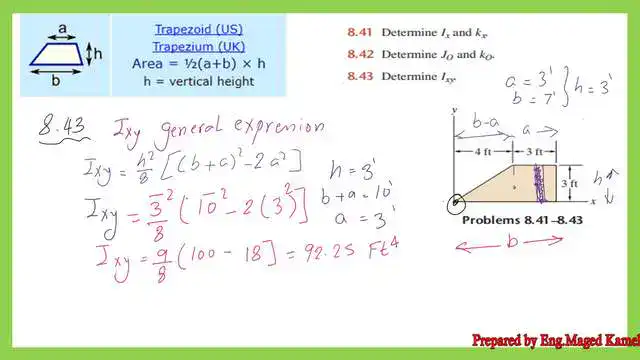
We can substitute the values of b, a, and h, and obtain the final value of Ixy as 92.25 ft^4, which is the same as the value we obtained earlier. For more details, please refer to the next slide image.
The second practice problem for inertia is 8.48. Find Ixy for a given trapezium about the Cg.
For the second practice problem 8.48 of the two practice problems for Ixy for a trapezium, it is required to find the Ixy value for the trapezium at the Cg.
We have obtained the Cg distance values from the external axes x̄ and ȳ in the previous posts, and the trapezium has an area of 15 ft². The product of inertia about the Cg is equal to Ixy minus the product of area by (xbar*ybar). The final value of Ixy at the Cg is 7.10 ft4.
We ended after solving the two Practice problems for Ixy for a trapezium.
Thank you very much, and I look forward to seeing you in the next post.
Please refer to post 19 for more information about Ix for a trapezium.
Please refer to post 22 for more information about Iy for a trapezium.
The previous post, Post 26-Two: Practice Problems for the Polar Inertia of a Trapezium.
A useful external resource for the area, Cg, and inertia for the parallelogram, please refer to this link.
A new subject for maximum and minimum moment of inertia will be followed. Please refer to post 1; Easy illustration of the theory of pure bending.