24- Ix for the Trapezium second option

Last Updated on January 2, 2026 by Maged kamel

In the second option for Ix for the Trapezium, instead of dividing the Trapezium into one rectangle and two angles to determine the moment of inertia Iy, we will use a horizontal strip and integrate to get the moment of inertia about the x-axis.

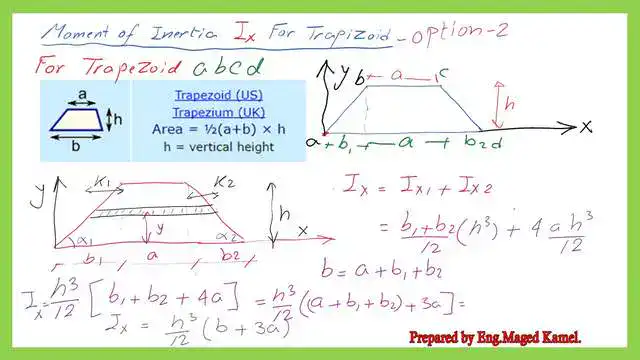
Ix for the Trapezium second option.

Derive the expression for k1 for the horizontal strip distance from the trapezium’s left upper corner to the strip’s left end.

We will use a horizontal strip of width dy for the Ix for the trapezium, the second option. The strip is located at y distance from the Trapezium, which has a length of (k1+a+k2), where a is the top length of the trapezium.

For a rectangle of base b, we want to get an expression for the value of k1. We consider the left triangle with a base of b1 and a height of h. Using the relation of (k1/b1)=(h-y)/h to get the K1 value, K1 can be written as equals b1*(h-y)/h. Please refer to the next slide image for more details.

Derive the expression for k2 for the horizontal strip distance from the trapezium’s right upper corner to the strip’s right end.

Similarly, we want the value of k2, which is the distance from the Trapezium’s upper-right corner to the end of the horizontal strip. We refer to the right triangle with a base of b2 and a height of h. We use the relation of (k2/b2)=(h-y)/h to get the k2 value. K2 can be written as equals b2*(h-y)/h. Please refer to the next slide image for more details.

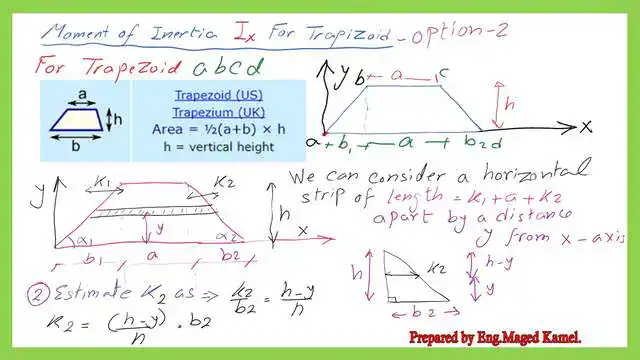
Integrate the horizontal strip from the bottom to the top of the Trapezium.

The moment of inertia Ix for the Trapezium second option can be obtained by integrating the horizontal strip from y=0 to y=h, where h is the height of the trapezium. The length of the horizontal strip can be written as equal to (a+b1+b2)=(a+b1*(h-y)/h+b2*(h-y)/h).

The inertia of the strip  dIx=(a+b1*(h-y)/h+b2*(h-y)/h)*y^2*dy, where dy is the width of the strip.

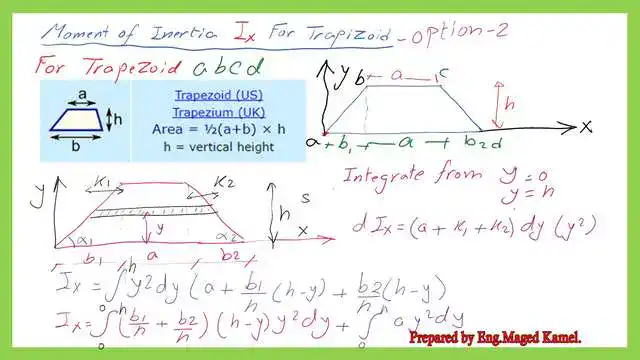
We can simplify the expression as composed of two items Ix1 plus Ix2. We can clarify the standard terms and arrive at the expression shown in the next slide. Ix1 can be written as (b1+b2)*h^3/12, where b1 is the distance from the lower left corner to the upper left corner of the trapezium. The distance b2 is the distance from the lower-right corner to the upper-right corner of the Trapezium.

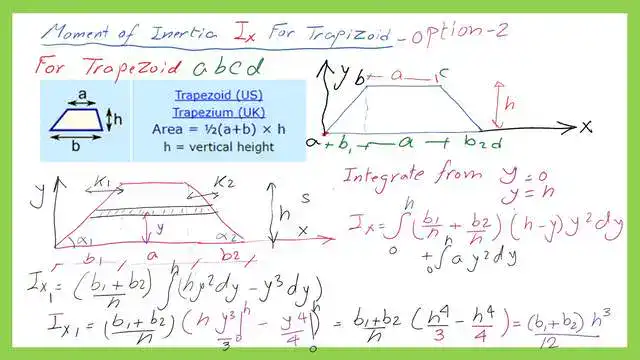
We can clarify the standard terms and obtain the expression shown in the next slide. Ix2 can be written as (4*a*h3)/12, where a is the length of the upper part of the trapezium and h is the trapezium height. Please refer to the next image for more details.

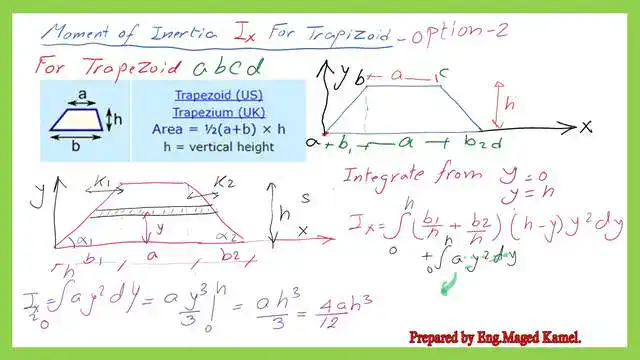
Derive the final expression for Ix for the Trapezium second option about the lower external x-axis.

We can add Ix1 and Ix2 to obtain the final expression for Ix for the Trapezium second option.

The Ix value for the trapezium can be expressed as equal to h^3*(b+3a)/12, where a is the length of the upper part of the trapezium, b is the lower base length, and h is the trapezium height—the same value estimated per the previous post 22. In the next post, we will solve two practice problems on the moment of inertia Ix for a trapezium. Thank you.

You can download and review the content of this post through the following pdf file.

Please find  Moments of Inertia – Reference Table for a calculator for various shapes.

This is a link to the complete details of how to get an x-bar and y-bar for a Trapezium.

This is the next post. Two practice problems for trapezium are for inertia.