7A-Solved problem-8 by Modified Newton-Raphson method

Last Updated on January 19, 2026 by Maged kamel

Solved problem-8 by Modified Newton-Raphson method.

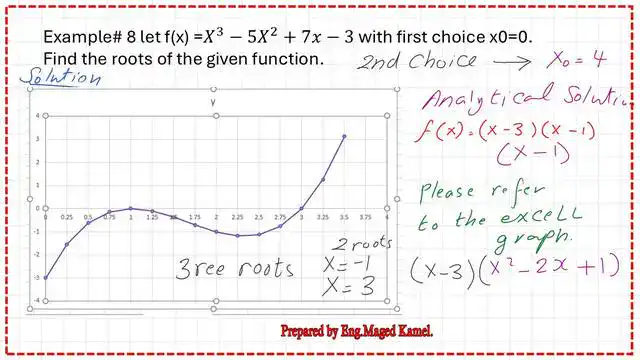
For the given Solved problem-8 by the Modified Newton-Raphson method. The function f(x)=X^3-5*X^2+7x-3 with the first choice of x₀=0. The following slide includes the formula for the Modified Newton-Raphson method.

From the graph (next slide), we can see that there are three roots: x1 = 3, x2 = 1, and x3 = 1, as shown in the Excel sheet for Solved problem-8 using the Modified Newton-Raphson method. The x=0 will give a negative value of -3.

1-We start to use the modified Newton-Raphson method, consider the initial point x0 equals 0, and we start to find the expressions for f(x),f'(x), f’^2(x), and f”(x).

2- Substitute at x=0 and get the values for f (0), f'(0) & f’^2(0), and f”(0). The value of f(0)=-3. The value of f'(0)=7.

The value of f”(0)=-10. Substituting into the equation of the modified Newton-Raphson method, we get x1 = 1.10526. Please refer to the next slide image for a detailed estimation of the various parameters.

We plug in x = 1.105263 and get the corresponding values of f(1.105263), f'(1.105263), and f”(1.105263).

4- Substitute in the modified Newton-Raphson method. We get a new point with x2 = 1.00. and again continue to estimate f(1.00) and f'(1.00), and then apply them in the equation to get a new point that will be point x₃.

5-Continue the process until x converges to 1.00. The Excel sheet for the various values of x, based on the modified Newton-Raphson method from x₀=0 till x₄=1.00, is shown.  

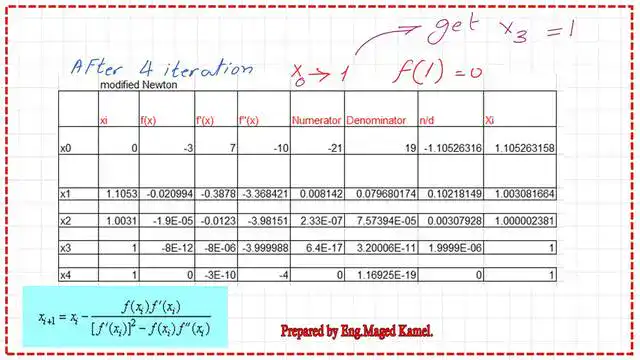
This table shows the number of iterations and the corresponding f(x), f'(x), and f”(x) for each case. 

Solved problem-8 by Modified Newton-Raphson method using x₀=4

Now if we consider the starting point as x₀=4.00, and proceed to get the x value for f(x)& f'(x) , f’^2(x) and f”(x) for x0=4.00. We have f(4)=9,f'(4)=15 and f”(4)=14. The value of x1 is found to be=2.6363.      

2- Substitute at x₁=2.6363 and get the values for f (2.6363), f'(2.6363)  & f”(2.6363). The values are shown in the next slide image.

3-Plug in the previous calculation into the Modified Newton-Raphson equation and substitute the value of X2. Substitute x2 = 2.8202 and get the values for f(2.6363), f'(2.8202) & f”^2(2.8202), f”(2.8202), and x3 = 2.9617.

This is the Excel sheet for the calculation based on the Modified Newton Raphson Method, starting from x₀=4 till x5=3.00.

Solved problem-8 by Newton Raphson method with x₀=0.

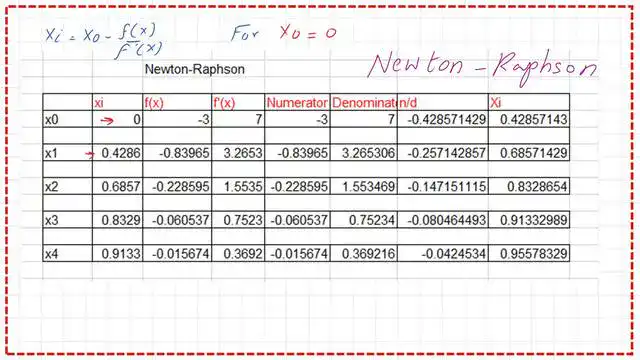
This is a comparison of the Newton-Raphson method without modification for problem 8, based on the Newton formula. Starting as before with x0=0 and using the equation of xi=x0-(F(x0)/f'(x0)

We can get the x1 value to 0.4285, then substitute to get x2 = 0.6857.

This is an Excel sheet for the points that are obtained by using the Newton-Raphson method for the Solved problem-8

The initial point is (0). The table lists all the values of the function till point x4. That point will be equal to 0.95578.

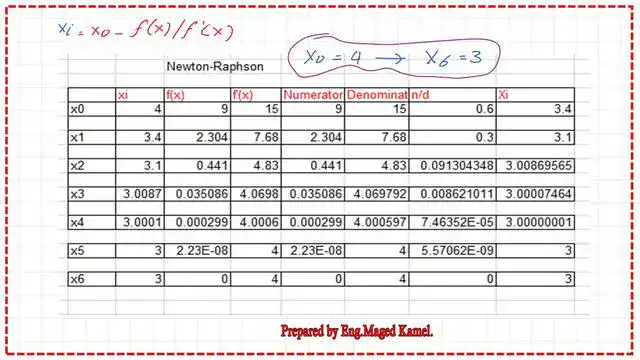
If we start with x₀=4.00 to get the other root but based on the Newton-Raphson method. The Excel sheet with more details shows the different values of x.

This is an Excel sheet for the points obtained, considering the initial point x0 = 4.00, and ending with point x6 = 3.

This is a comparison between the Newton-Raphson and Modified Newton-Raphson methods for problem 8, using an Excel sheet.

The PDF file containing the content of this post can be viewed or downloaded from the following link.

The next post is Structural analysis numerically by the Newton-Raphson method.

This is a useful link for a numerical analysis calculator.