2- Types of Matrices: An Easy Introduction to Their Forms.

Last Updated on March 24, 2025 by Maged kamel

Types of matrices-part 2.

Scalar matrix, Symmetric matrix.

The scalar matrix, the first item is the matrix where the diagonal is a scalar. For the given matrix, the diagonal is =2, while the remaining elements are all zeros. There are three rows and three columns, so the matrix dimension is 3×3.

The second item of the types of matrices is the symmetric matrix. From its name, a matrix is a symmetrical matrix about the diagonal.

For every I,j  aji=aij, for an element above the diagonal element, second row, second column element, a22, we have a12=-3, equal to the component to the left of a₂₂,  which is a₂₁, with no change of signs. Similarly, a23=a32=+7, where a23 is at the second and third columns, while a32 is the element at the third row and second columns.

So we will find that aij=aji, a₂₁=a_12, and a₂₃=a₃₂, a₂₁=-3, the element in the second row, with the first column.

While a₁₂=-3, which is the first row, with the second column. a₂₃=7=a₃₂, which is this element, the third row with the second column.

What is the unit matrix-identity matrix?

What is the unit matrix? The unit matrix is the third of the types of matrices. It is a matrix in which all diagonal elements are equal to 0. The diagonal equals 1. The unit matrix is also called the identity matrix. Unit matrix is used as the multiplicative identity of square matrices in the matrices concept.

As we can see in the next slide image, we have a 3×3 matrix.

While the other remaining elements are zeros. 
What is the skew-symmetric matrix? It is the matrix for which a =-aji. So for a₂₁=-a₁₂, a₂₃=-a₃₂. In brief, elements are symmetric but change in signs.

What is the triangular matrix?

The 4rth item of the types of matrices is the Triangular Matrix or the echelon form. The matrix consists of one of two forms: the first form is the upper triangular matrix or a lower triangular matrix. The main difference can be shown as follows.

For the given matrix, we have a 3×3 matrix. The elements of the diagonal are 1,4,6. The elements above the diagonal are 3,2,1. The elements below the diagonal are all zeros. The other form is the lower matrix.

The lower matrix has elements of zero values above the diagonal elements, while other elements below the diagonal have values. The expression for the lower matrix can be written as a for i> or j, which means that, in this case, it has a value.

While aij=0 for i<j. For instance, a₂₃ or the second row with the third column, for which i, or the row number is < j which is the column number.

When the row number i is bigger than or equal to the column number j, elements a31,a32, and a₃₃ will have values.

The first-row elements are (2 00), the second-row elements are (4 2 0), and the third-row elements are(0 0 6).

The upper matrix has a definition opposite to the lower matrix’s definition. The elements below the diagonal are all zeros, while those above the diagonal are non-zero.
 The first-row elements are (1 3 2), the second-row elements are (0 4 1), and the third-row elements are(5 8 2).

Transpose of matrix.

For the transpose of a matrix, we let the rows change to columns and change the columns to rows. We have a matrix A, where the first row is( 2 5 4), the second row is(7 6 8), and the third row is ( 2 7 6).

The transpose of a matrix is called “A transpose.” It has a first row, the same as the first column of Matrix A. The first row is (2,7,2); as we can see, the second row will be (5,6,3), the second column of Matrix A. The third row is the same as the third column in Matrix A, for which the values are (4,8,6).

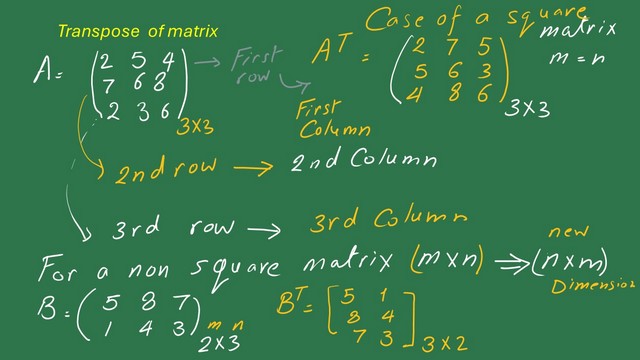
Press on any image, and you will see a slide show of pictures from 1 to 2, which are included above.

For a valid external link, math is fun for the matrix part.
The following post, Matrix operation-part-1. The post includes the addition and subtraction of two matrices, the scalar product.

This is a link to the matrix calculator.