Last Updated on August 31, 2024 by Maged kamel

Practice problem 5-5-6-Compute Lp and Lr, φb*Mn and Mn/Ωb for lb=10 feet.

Practice problem 5-5-6 A W12 x 30 of A992 steel has an unbraced length of 10 feet. Using Cb = 1.0, a. Compute Lp and Lr. Use the equations in Chapter F of the AISC Specification. Do not use any of the design aids in the Manual.
b. Compute the flexural design strength, φb*Mn.
c. Compute the allowable flexural strength Mn/Ωb. Practice problem 5-5-6 is from the Steel Design Handbook.

How do we estimate Lp for W12x30?

In the absence of design aids, Table 3-3, where W sections are sorted by their plastic section Zx, in which we can easily find the values of lp and lr and other values of flexure design moments, We need to estimate Lp and lr values by using the equations given by the specifications.

The following slide shows The detailed estimate of the Lp value; Lp is the value of the un-braced length that the plastic hinge should be developed, which is given by equation F2-5 as equal to 1.76*rysqrt(E/Fy).

From Table 1-1, we will get the radius of gyration ry for W12x30. The ry value is 1.52 inches. From the data on A992 steel, we have the yield stress Fy=50 ksi. The E value is 29000 ksi. The value of Lp will be 64.43 inches and can be rounded to 5.40 feet.

How do we estimate Lr for W12x30?

We use table 1-1 for W section W12x30 to get the necessary data for estimating the Lr. Lr represents the unbraced length at which lateral-torsional buckling transitions from the inelastic range to the elastic range. These items are ry, rts, Zx,SX, Cw,C, J, H0.

We can get the value of bf/2tf and h/tw. Please refer to the next slide image for details.

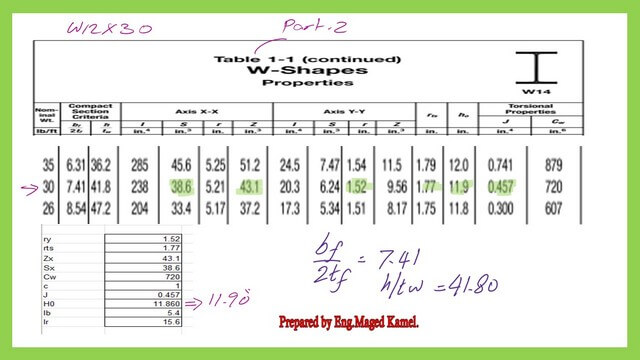
What is the value of lr?

We use the equation F2-6 provided by the AISC specification. The value of lr equals 187.24 inches and is rounded to 15.60 feet. Please refer to the next slide image for more details. Thus, we have completed the required part a) in the practice problem 5-5-6.

Check buckling parameters for W12x30 where Fy=50 ksi.

We will find the local buckling parameters for the flange and web-based Fy=50 ksi. Based on item 10 in Table B4.1b, the flange λFp=0.38*sqrt(E/Fy), since we have E29000 ksi and the given Fy=50 ksi, then λFp=0.38*sqrt(29000/50)=9.15. λFr=1.0*sqrt(E/Fy)=1*sqrt(29000/50)=24.08.

for the web compactness ratio, the flange λwp=3.76*sqrt(E/Fy), λWp=3.76*sqrt(29000/50)=90.55. λwr=5.70*sqrt(E/Fy)=5.70*sqrt(29000/50)=137.27. Please refer to the next slide image for the detailed estimate of compactness ratios.

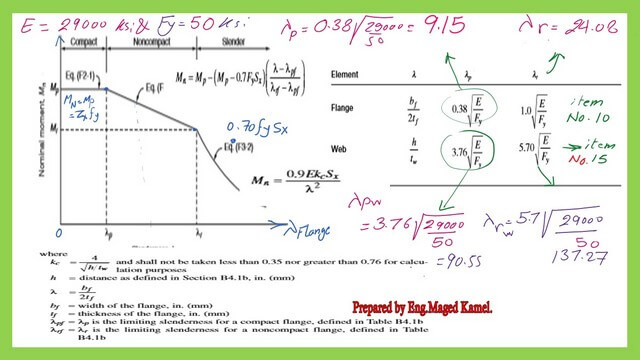
Check whether W12x30 is compact or non-compact.

In the next slide image, we have the values of bf/2tf and h/tw of W12x30 against the required local buckling parameters based on Fy=50 ksi. We will find out that the flange and web are compact, so the whole section of W12x30 is compact.

Find the equation of Mn-based on Fy=50ksi.

The Plastic moment value equals Zx*Fy, which is equal to 50×43.10=2155 inch. kips. The term (0.7*Fy*Sx) value equals 0.7*50*38.60=1352 inch. kips. The first term corresponds to bracing length Lp=5.40 ft; the second corresponds to lr=15.60 feet. We have a given lb=10 ft.

We get the values of Mp and 0.70*Fy Sx in Ft.kips by using the conversion factor of 1Ft=12 inches. Mp value equals 179.583 Ft. kips, while 0.70*Fy Sx=112.583, we could round these values to the nearest ones.

There is a linear relation for the required Mn with Mp and(0.7*Fy*Sx) together with Lp and Lr. The BF factor is the slope value which equals (Mp-0.7*Fy*Sx)/(Lr-Lp)=6.5686.

What is the value of Mn at lb=10 feet?

The relation of 179.583-6.53*(Lb-Lp) represents the nominal moment value. The Lb value equals 10 feet, and the Lp value equals 5.40 feet. The Final value for Mn equals 149.367 Ft. kips.

Part b) Compute the Flexural design strength-φb*Mn.

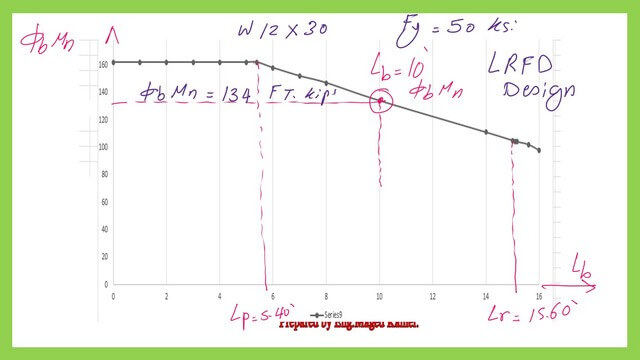
For part b of the practice problem 5-5-6, for Flexural design strength-φb*Mn, we multiply the Nominal value by the factor φb, which equals 0.90. We get the value of 134 ft.kips.

Part c. Compute the allowable flexural strength Mn/Ωb.

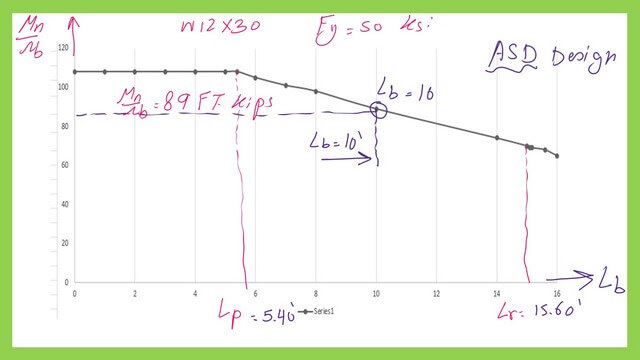
For part b of practice problem 5-5-6, for allowable flexural strength Mn/Ωb, we multiply the Nominal value by the factor (1/ Ωb), which equals (1/1.67). We get the value of 89 Ft.kips.

We could use an Excel sheet to graph the relation between Lb and the Flexural design strength-φb*Mn for W12x30 Fy=50 ksi. We can see the linear portion and the Value of φb*Mn at 10 feet equals 134 ft. kips.

We could use an Excel sheet to graph the relation between Lb and allowable flexural strength Mn/Ωb for W12x30 and Fy=50 ksi. We can see the linear portion and the Value of Mn/Ωb at bracing length 10 feet equals 89 ft. kips. Thanks a lot.

Here is the link for Chapter 8 – Bending Members.
This links to the next post, Practice problem 5-5-8-Compute Mn.