Last Updated on September 22, 2024 by Maged kamel

Solved problem-case-2- Mohr’s circle of inertia.

Post content.

In this post, we will introduce a solved problem-case-2-Mohr’s circle of inertia, where Ix is lesser than Iy and the product of inertia Ixy is positive.

For a given Area the following data are presented as follows: the moment of inertia Ix is 14 inch4. the moment of inertia about y-axis Iy is 24 inch4. The product of inertia Ixy is 12 inch4.

It is required to determine the principal moment of inertia and the angle alpha that the x-axis makes with the maximum moment of inertia.

In the first slide, I have evaluated the coordinates of points A, and B, as well as the radius R which we will use to draw Mohr’s circle of inertia.

Solved problem-case-2-Mohr’s circle of inertia-drawing the circle.

For the Solved problem-case-2-Mohr’s circle of inertia, We start by drawing two intersecting axes. The horizontal axis represents the value of the moment of inertia. The vertical axis represents the value of the product of inertia, with a positive value pointing up. One unit represents 1 inch4.

We start by locating Point A, which has Ix, Ixy values as(14,12) units and will be located above the axis of inertia by a value of positive Ixy equals 12 units, and apart from the vertical axis Ixy by a distance of (14) units.

Similarly, we can draw point B, which has a coordinate of (Iy,-Ixy). In units will be (24,-12), for the negative value the point will be below the axis of inertia by 12 units and apart from the vertical axis by the positive value of 24 units. We will join both two points, The line AB will intersect the horizontal axis at point O, which will be the center of the circle.

We can draw the circle by getting the middle point O, which has a coordinate of 0.50*(Ix+Iy), from the given data this value is equal to (14+24)*0.50=19 units.

The radius of the circle is estimated from the equation, R=sqrt ((Iy-Ix)^2+Ixy^2), this is applied since Iy is bigger than Ix. We have Ix=14 inch4.Iy=24 inch4.Ixy=12 inch4. We can use the data to get the radius of Mohr’s circle of inertia, applying the known formula, we can get the radius value equal to 13 inch4. Please refer to the slide image for more details.

This is How to get the value of 2θp1 for the Solved problem for A Solved problem-case-2-Mohr’s circle of inertia.

To get the maximum value of inertia Imax we can add the value of the radius of the circle to the value of the center point, the maximum value of the moment of inertia is equal to (19+13)=32 units, and the product of inertia is zero, this point is point E.

For the minimum value of inertia, the value will be equal to the (0.50*(Ix+Iy)-R, where R is the radius value.

I minimum is equal to 6 units, the product of inertia is equal to zero, and the point of minimum value of inertia is point C.

Solved problem-case-2-Mohr’s circle of inertia-direction of principal axes U&V.

To draw the direction of the major axis U in Mohr’s circle of inertia, we will locate point A’, which is the mirror point of Point A. Point A’ has a coordinate of (10,-12) units. we will join point O, and with point A’ we will get the direction of the major Axis U.

To draw the direction of the major axis V in Mohr’s circle of inertia, we will locate point B’, which is the mirror point of Point B. Point B’ has a coordinate of (24,+12) units. we will join point O, and with point B’ we will get the direction of the major Axis V.

The directions of U and V for the normal view.

Draw a line from point C to A’ , this is the direction of the U-axis in the normal view. Draw a line from C to point B’ this is the direction of V -axis in the normal view.

Solved problem-case-2-Mohr’s circle of inertia using general expression.

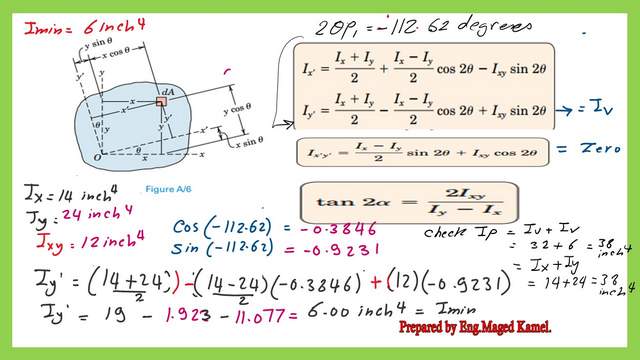
We can use the general expression for Ix’ to check the value of Imax, provided that when the angle 2θ = (2φp1), which is (-112.62 degrees ), Ix’ value will be equal to Imax. We plug in with Ix value=14 inch4, Iy value=24 inch4 and Ixy=12 inch4.

The value of Ix’=32 inch4 is the same as Imax estimated by the use of Mohr’s circle.

We can use the general expression for Iy’ to check the value of Imin, provided that when the angle 2θ = (2φp1), which is (-112.62 degrees ), Iy’ value will be equal to Imin. We plug in with Ix value=14 inch4, Iy value=24 inch4, and Ixy=12 inch4.

The value of Iy’=6.0 inch4 is the same as Imin estimated by the use of Mohr’s circle.

It is important to check that the sum of Ix and Iy, will be the same value of the sum of Iu and Iv, where Iu is the maximum value of inertia, While Iv is the minimum value of inertia. Ix+Iy=14+24=38 inch4. imin+Imax=6+32=38 inch4.

Oriented datums to let x-direction as a horizontal axis.

To let the x-axis as horizontal Mohr’s circle of inertia, the x-axis is represented by line OE. The datums of Ix&Ixy are adjusted to represent the direction of U.

Line OE represents the x-direction concerning two new datums which are shown in the next slide image. Line OC represents the Y-direction concerning two new datums. The full data that covers our Solved problem case-1-Mohr’s circle of inertia is included in the slide image.

The following post will discuss Mohr’s circle of inertia-third case.

There is a video illustrating the content of this post-introduction video for Mohr’s Circle of Inertia.

This is a link to a useful external resource: a calculator for Cross Section, Mass, Axial and polar area moment of Inertia, and Section Modulus.