Last Updated on September 22, 2024 by Maged kamel
Mohr’s circle of inertia-third case.
Content of the post.
In this post, we will be talking about Mohr’s circle of inertia-third case. Mohr’s circle of inertia-third case is the case where the moment of inertia about the x-axis is bigger than the moment of inertia about axis Y, and the product of inertia Ixy is negative.
We expect that the tangent value of 2θp is positive from the equation of tan 2θp since Ixy is negative. Two examples of shapes that satisfy the requirements of Ix, Iy, and Ixy which are the unequal angle with b>a, we consider the Ix, Iy, and Ixy about the Cg, in this case, we use b to raise the vertical distance b to the power of 3, which will lead to an increase in Ix value.
The second example is the right angle triangle case 1, where Ix >Iy and Ixy is negative at the Cg. We have Ix at Cg equals b*h^3/36, while the value of Iy at the Cg will be equal to h*b^3/12. The product of inertia Ixy value will be found to be equal to -b^2*h^2/72.
What is the orientation of the principal axes for Mohr’s circle of inertia-third case?
We have the general expression for the moment of inertia for any oriented axis, we call it Ix’. For Mohr’s circle of the inertia-third case, the value can be a maximum value when the angle 2θ has a cosine of a positive value and the sine value is also positive, this angle is called 2θ.
For a positive 2θ, Its sine and cosine will be positive. This angle is measured from the X-axis to axis U in the anticlockwise direction. If we check Ix’ expression when Ix is bigger than Iy, the first term (Ix+Iy)/2 will be positive. The second term which is (Ix-Iy)/2* cos 2θ, will be positive too.
For the third item (-Ixy*sin(2θ), it will (negative) be multiplied by a negative, and the result will be positive. The next slide image shows how to derive the expression.
For Mohr’s circle of the inertia-third case, the value of Ix’ can be a minimal value when the angle 2θp2 has a cosine of a negative value and the sine value is also negative. This angle is measured from the X-axis to axis V, in the clockwise direction. based on the next slide, both negative values are to be achieved if the angle 2θp2 exists in the third quarter. Both the U and v axes are shown in the next slide.
When Iy’ value can be maximum or minimum?
For Mohr’s circle of the inertia-third case, the value for Iy’ can be a maximum value when the angle 2θp2 has a cosine of a negative value and the sine value is also negative. This angle is measured from the Y-axis to U axis. The next slide image shows how to derive the expression.
For Mohr’s circle of the inertia-third case, the value for Iy’ can be minimal when the angle 2θp1 has a cosine and also sine of a positive value. This angle is measured from the Y-axis to V axis. The next slide image shows how to derive the expression.
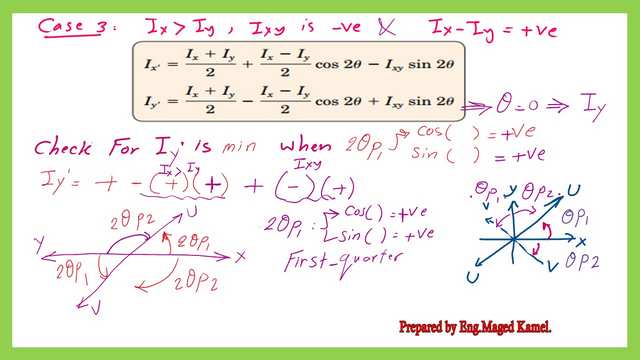
In the next post, we will continue with part 2 to show how to draw Mohr’s circle of inertia-case 3.
This is a link to a useful external resource. Calculator for Cross Section, Mass, Axial and Polar Area Moment of Inertia, and Section Modulus.


