Definition of Interpolation, what is linear interpolation?
As defined by Prof. Gilat Amos, reference book, Numerical Methods for Engineers and Scientists, 3rd Edition: An Introduction with Applications Using MATLAB, Interpolation is a procedure in which a mathematical formula is used to represent a given set of data points such that the formula gives the exact value at all the data points and an estimated value between the points.
This section shows how this is done using a single polynomial, regardless of the number of points. As was mentioned in the previous section, for any number of points n there is a polynomial of order n – 1 that passes through all of the points.
For two points the polynomial is of the first order (a straight line connecting the points). For three points the polynomial is of second order (a parabola that connects the points), and so on.
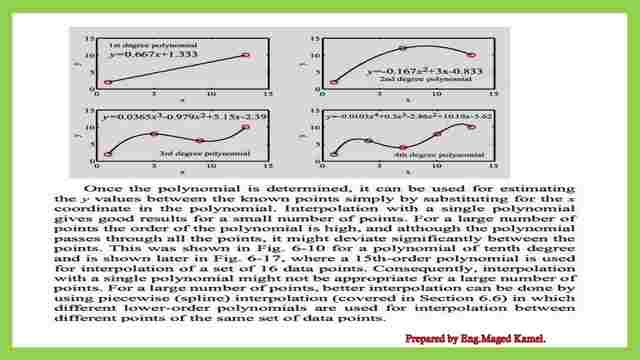

This is illustrated in Fig. 6-11 which shows how first, second, third, and fourth-order polynomials connect two, three, four, and five points, respectively.

What are polynomials?
From math is fun, site, The polynomial is composed of two words, poly (meaning “many”) and nominal (in this case meaning “term”), so it says “many terms”.
A polynomial can have constants, variables, and exponents, but never division by a variable.
In the next slide image, the first-degree polynomial is composed of two terms, one term is a constant while the other term is with a variable. there are second-degree-third-degree polynomials expressed.


What is the leading coefficient for a polynomial?
The leading coefficient of a polynomial is the coefficient with the highest variable degree. here is the polynomial calculator for the DEGREE AND LEADING COEFFICIENT CALCULATOR.


A Solved problem for leading coefficient and leading term.
For a given example of f(x)=5x^4+2x^3-x+4, the leading coefficient is the coefficient with the highest power, the highest power is 4, the coefficient of that highest power is 5, while the highest term is(5*x^4).


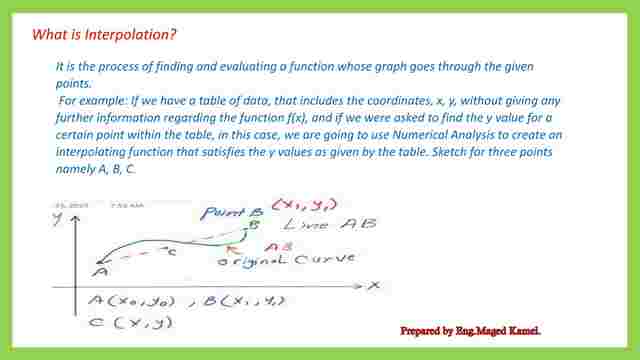
What is linear interpolation?
Linear interpolation is the process of estimating a missing functional value between two data points by constructing a line between these two points. The linear function of the line can then be used to find the desired value of the data point of interest.
Using the initial point A which has a coordinate of (x0,y0), and another point b with a coordinate (x1,y1), the line joining the two points can be estimated by estimating its sloe as the difference in y divided by the difference in x distance.
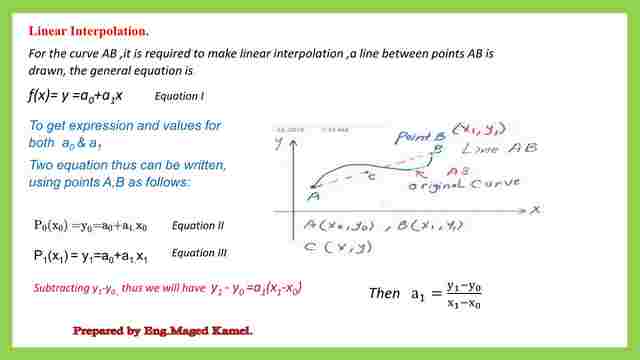

The final form of the polynomial used for the linear interpolation can be written as P(x)=y=y0+((y1-y0)*(x-x0)/(x1-x0).
Then we will substitute by the given values of points A and b, thus we get the final equation of x and y.


Solved example#1.
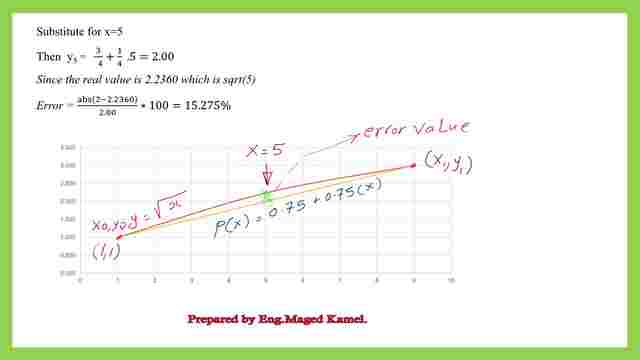
if we want to get a linear interpolation of the f(x) sqrt(x), we need two points, which are given by point-1, with (1,1) and the second point is point 2, which has a coordinate of(9,3).
We will substitute in the equation of the P(x)=y=y0+((y1-y0)*(x-x0)/(x1-x0). for x0=1, y0=1 and (x1=9, y1=3), thus we can get the final polynomial equation as a linear interpolation.


For point c where x=5, we can p(5) as=2.00, for f(x) as sqrt of (5) it will be equal =2.236, we can estimate the error between the original function and the linear interpolation function, a graph is drawn to show the difference between the two functions.

This is a link to the pdf file used to illustrate this post.
The next post is an Easy introduction to quadratic interpolation to quadratic interpolation.
This is a great resource for the background of interpolation.
Linear interpolation calculator tool.

