Last Updated on September 9, 2026 by Maged kamel
Solved Problem: For the design strength of the tension member.
Limit states for tension members.
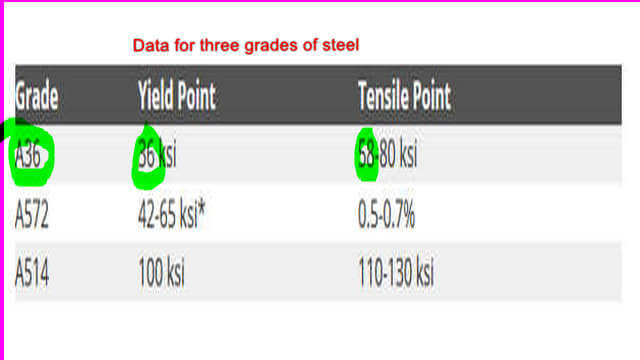
Limit state of Yielding and rupture and the corresponding values for φt= 0.75 and Ωt=2.00 for each case.
This table includes the various values for Fy and Fult; for ASTM A 36 and ASTM A 572, the grade should be specified as Fy = 42 ksi to 65 ksi; for ASTM A514, Fy = 100 ksi.
A solved problem 3-6-tensile strength for W section-bolted at flanges.
Solved Problem 3-6 determines the LRFD design tensile strength and the ASD allowable design tensile strength for a W10x45 with two lines of 3/4-inch-diameter bolts in each Flange, using ASTM A572 Grade 50 (Fy = 50 ksi, Fu = 65 ksi) and the AISC Specification.
Each line has 3 bolts for both the upper and lower Flange. Our first step is to get the Area of the W section by using the relevant table for W10-45.
The Area Ag = 13.30 in^2. The diameter of each bolt is 3/4 inch. If we add 1/8 inch, the overall diameter will be 7/8 inch.
Back to the statement of this solved problem, we assume at least three bolts. The table includes an item stating “At least three bolts and more.” We can obtain the U value from the table.
Design strength by Yielding for W section-LRFD-ASD.
We can evaluate the LRFD for ASD tensile strength by using the Yielding method, as shown in the following picture, for problems 3-6. In that calculation, we need only the gross Area of the given section.
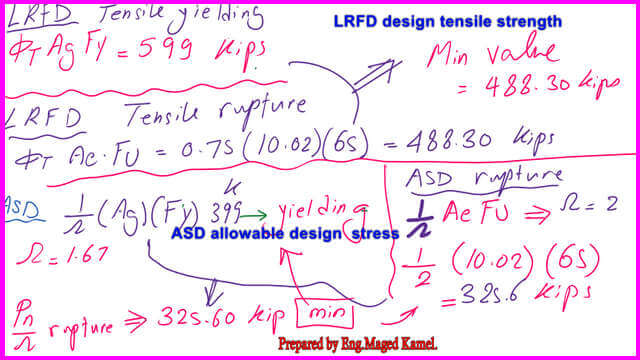
For LRFD, Ag=3.30 inch2, Fy=50 ksi, φt =0.90, the φt *Pn=0.9*3.30*50=599 kips. This is the LRFD Nominal strength for design based on Yielding.
For ASD, Ag=3.30 inch2, Fult=50 ksi,1/ Ωt =1/1.67, the 1/ Ωt *Pn=(1/1.67)*3.30*50=399 kips. This is the ASD Nominal strength for design based on Yielding.
How do we estimate the shear lag factor, U, for the W section?
To estimate U for W10x45, we convert it to two WT 5×22.50, obtain the y-bar value (0.907), and use it as x-bar in the equation U = (1 – x̅ / L). Use the equation U=(1- x̅ /L), and then substitute by x̅ =0.907, we get U=0.8867.This is Case 2 for the shear lag factor value.
We can also determine the shear lag factor from Case 7 for three or more fasteners.
If we use the tables for three fasteners with bf/d > 2/3, we have U = 0.90, which is higher than the previous value of U and therefore can be used.
We have 4 bolts, 2 at the top Flange and the other two at the lower Flange; our bolt diameter is 7/8 inch, and T flange=0.62″. We can estimate Ant=Agross-4*(7/8)*0.62=13.30-4*7/8*0.62 =11.13 inch2, Fult=65 ksi, as given in the solved problem.
After selecting the larger value of U, which is 0.90, we can determine the effective Area.
For Aeff=Anet*U=11.13*0.90=10.02 inch2.
Tensile Yielding by LRFD= φ*Fy*Ag=599 kips, while Tensile rupture by LRFD can be estimated as φt*A eff*Fult=0.75*10.02*65=488.30 kips. For the LRFD tensile strength, take the minimum value of the LRFD Limit states for Yielding and rupture as follows: φt*Pn=min of (599, 488.30)=488.30 kips.
Tensile Yielding by ASD= 1/Ωt*Fy*Ag=399 kips, while for tensile rupture by the ASD, it can be estimated as 1/Ωt*A eff*U*Fult=(1/2)*10.02*65=325.65 kips.
For the ASD tensile strength, take the minimum value of the ASD Limit states for Yielding and rupture as follows: (Pn/Ωt)=min(399, 325.6)=325.60 kips.
You can view or download the PDF file for this post from the following document.
For a more detailed illustration of block shear, there is a very useful external link to Chapter 3, Tension Members—a Beginner’s Guide to the Steel Construction Manual, 14th ed.
Chapter 3 – Tension Members– A Beginner’s Guide to Structural Engineering is a great external resource.—aBeginner’s Guide to the Steel Construction Manual, 15th ed.
A useful external link: Tensile Yielding and tensile rupture. A Beginner’s Guide to the Steel Construction Manual, 16th ed.
For the next post: a solved problem 4-2 on shear Lag factor U.