Last Updated on November 13, 2024 by Maged kamel

Part 2 of Practice problem-7-38 Discontinuity Functions.

Part 2 of practice problems 7-38 involves drawing the shear-force and Moment diagrams for a given beam acted upon by two vertical loads.

The practice problem is included in Prof. Timothy Philpot’s book An Integrated Learning System, Mechanics of Materials. The same problem is P 7-62 in the third edition.

We have a given beam, a given simply supported beam with a span of 20 feet. A downward load of 3000 Lb acts at x=5 feet from the left support.

Simultaneously, one concentrated moment of 8000 lb. ft acts anticlockwise. The downward uniform load of 800 lb/ft has a limited width of 7 feet starting from x=9 ft. 

What are the cases that P7-38 covers regarding the discontinuity function in the table?

This problem covers cases 1,2 and 5 from the discontinuity table.

 Part a) requires using the discontinuity function to write the expression for load w(x) in part a) and to include the beam reaction in the expression.

In part b), w(x) must be integrated twice to determine the V(x) and M(x).

In part c), V(x) and M(x) must be used to plot shear force and bending moment diagrams.

Use an Excel sheet to find the values of reactions.

This is the Excel sheet I have used: the sum of an Ay +Ey=8600 Lbs, which is 3000 lb+ 800 * 7=8600 lbs.

We get the AY value by taking the moment at E, and the Ay value equals 4750 lbs. From the sum of Y forces, we have Ey=8600-4750=3850 lbs.

Use the if-then function built in Excel for the shear expression for the beam.

Another check to get the Ey is by taking the moment to the left support, which will again give us the same 3850 lbs. These regions are from zero to 5, 5 to 9, 9 to 16, and 16 to 20 feet. 

The first column shows the x distance in feet, the second the shear Value in lbs, and the last the moment value in Lb.ft.

We have a drop at X equal to 5 feet.

We have a drop in shear by Value of 3000 lbs and a decline of moment value by 8000 lb.Ft. Also, again, there is a change in the slope at X = 9 ft—a drop of 800 lb/ft due to the distributed load.

How do we express the value of the shear and the value of the moment at the point of x=5? Please find the expression for shear.

=IF(AND(0<=A19,A19<=5),4750,IF(AND(5<A19,A19<=9),4750-3000,IF(AND(9<A19,A19<=16),4750-3000-800*(A19-9),IF(AND(16<A19,A19<=20),4750-3000-800*(A19-9)+800*(A19-16),0))))

There are two terms: one term for x<=5; in this term, the shear value equals 4750 lbs. Meanwhile, the second term is for X>5 and less than and equal to 9; the shear value is 4750-.3000.

The third term is for X>9 and less than and equal to 16; the shear value is 4750-3000-800*(A19-9).A19 is the cell for x value where x is 5 ft.

The fourth term is for X>16 and less than and equal to 20; the shear value is 4750-3000-800*(A19-9) + 800*(A19-16). A19 is the cell for the x value, where x is 5 ft.

I have added two cells for x=5. To create a step in the Excel shear at x=5, the upper cell B19 is for x<=5 in the expression. In the second cell, B20 is the expression for x<5 with no equal sign. 

For x=5 and x=5 plus, I put two values for 5, five here and five here. And in the expression.

We have A19 > or equal zero. For A19 < or equal 5, putting the equal sign here and Less than five is essential. 

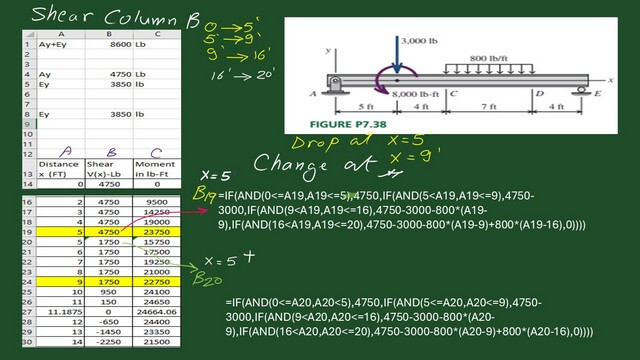
The next expression is for x=9 at cell B24.

=IF(AND(0<=A24,A24<=5),4750,IF(AND(5<A24,A24<=9),4750-3000,IF(AND(9<A24,A24<=16),4750-3000-800*(A24-9),IF(AND(16<A24,A24<=20),4750-3000-800*(A24-9)+800*(A24-16),0))))

Plot the shear force diagram for P7-38.

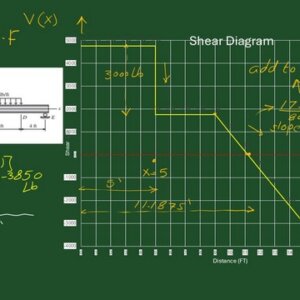
The following slide image shows the plot for the shear force diagram created using an Excel graph. The x-axis represents the distance in Feet, while the y-axis represents the corresponding shear Value.

Above the datum will be considered for the positive values, while below the datum represents the shear values with negative signs. We have a shear value of 4750 Lb,  from x=0 to x=5 feet.

Due to the concentrated load, we have a drop of 3000 lbs. So we have 4750-3000, and it will be 1750. Then comes the uniformly distributed load of 800 going downwards. We have a slope or drop of 800 lbs per foot. 

At X equal to 9 feet, We have 1750 going down with the slope of 800 lb per foot. So, to get the point where the shear equals 0, we can divide 1750 / 800 and get 2.1875 ft.

We add this Value to 9, and the final distance is 11.1875 ft. This is the distance to the point of zero shear. 

Please scroll to review all images in sequence.

Shear expression for x=5-P7-38.

Shear expression for x=9 ft by using if then function.

Part 2 of Practice problem-7-38-The shear diagram by using an excel sheet.

1/1

Use the if-then function built in Excel to get the expression for Moment.

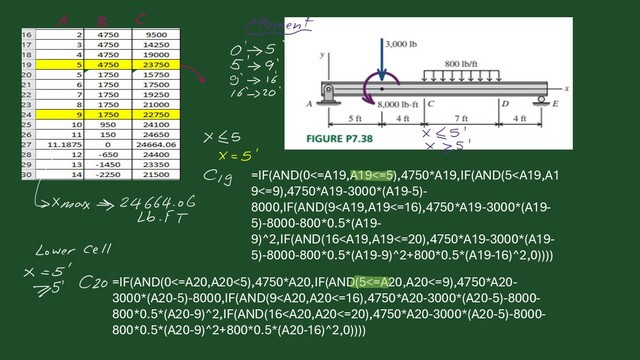
In the next slide image, there is an expression for M(x) using the if-then function in Excel. This is for the value of C19. We have a drop at the moment value at x=5 Ft. This is the first expression of<=5.

=IF(AND(0<=A19,A19<=5),4750*A19,IF(AND(5<A19,A19<=9),4750*A19-3000*(A19-5)-8000,IF(AND(9<A19,A19<=16),4750*A19-3000*(A19-5)-8000-800*0.5*(A19-9)^2,IF(AND(16<A19,A19<=20),4750*A19-3000*(A19-5)-8000-800*0.5*(A19-9)^2+800*0.5*(A19-16)^2,0))))

The 5<=A20 is adjusted for the Value of C20 to express the drop due to the moment of 8000 Lb.ft.

=IF(AND(0<=A20,A20<5),4750A20,IF(AND(5<=A20,A20<=9),4750A20-3000(A20-5)-8000,IF(AND(9A20-3000(A20-5)-8000-8000.5(A20-9)^2,IF(AND(16A20-3000(A20-5)-8000-8000.5(A20-9)^2+8000.5*(A20-16)^2,0)))).

Plot the Moment diagram.

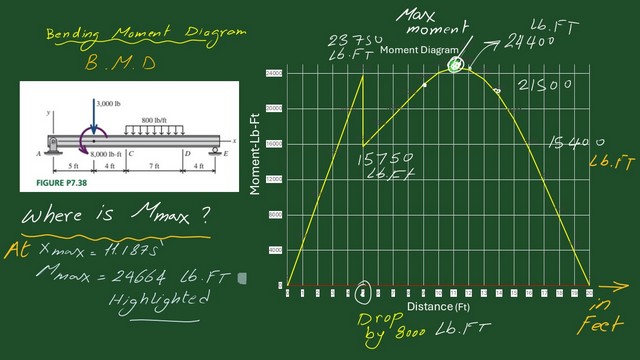
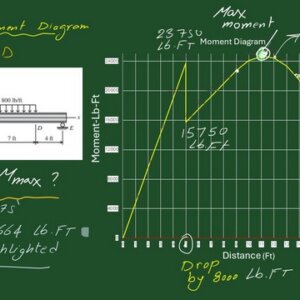
The sketch of the moment is drawn using an Excel graph.

We used this bending moment diagram, which we drew using the Excel sheet.

We started the moment at zero and then moved until X was equal to 5. At x=5, we have 23,750 lb .ft; due to the anticlockwise concentrated moment, there is a drop at X equal to 5, which equals 8000 LB .foot.

The Value of the moment after the drop equals 15,750 LB feet.

It starts from this point. We have a slope until the maximum moment, which is 24,664 Lb.ft. This point is at x=11.1875 Ft.

Please scroll to review all images in sequence.

The moment expression in excel using if then function.

Plot for Moment diagram P7-38.

1/1

We have come to the end of our discussion about 5a-Part 2 of Practice problem-7-38 Discontinuity Functions.

Thanks a lot.

The previous post is Part 1 of Practice problem-7-38 Discontinuity Functions.

There is a video for this post; this is the link.

The previous post is post 5, part 1 of Practice problem-7-38 Discontinuity Functions.

This is a link to my “ YouTube playlist” for Singularity functions.