Last Updated on October 12, 2024 by Maged kamel
Part 1 of Practice problem-7-38 Discontinuity Functions.
We will solve practice problem 7-38, which involve developing load function W(x), shear function V(x), and moment function M(x) using the discontinuity function. The same problem is P 7-62 in the third edition.
The practice problem is included in Prof. Timothy Philpot’s book, An Integrated Learning System, Mechanics of Materials.
We have a given beam, a given simply supported beam with a span of 20 feet.
A downward load of 3000 Lb acts at x=5 feet from the left support.
Simultaneously, one concentrated moment of 8000 lb.ft acts anticlockwise. The downward uniform load of 800 lb/ft has a limited width of 7 feet starting from x=9 ft.
This problem covers cases 1,2 and 5 from the discontinuity table.
Part a) requires using the discontinuity function to write the expression for load w(x) and to include the beam reaction in the expression. In Part B, W(X) is to be integrated twice to determine V(x) and M(x).
Part C needed V (x) and M(x) to plot shear force and bending moment diagrams.
There is also a limited width downward uniform load of 800 Lb/ft with a length of 7 feet starting from x=9 ft.
This problem covers cases Number 1,2, and 5 from the discontinuity table. Please refer to the next slide image for details on cases 1 and 2.
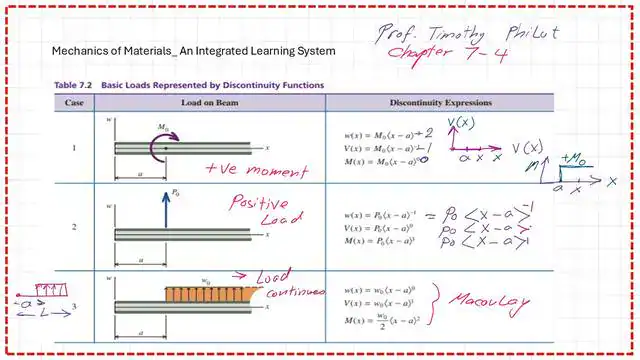
Please refer to the next slide image for details on case 5.
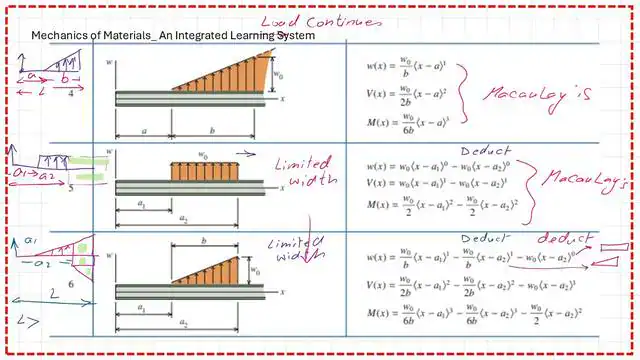
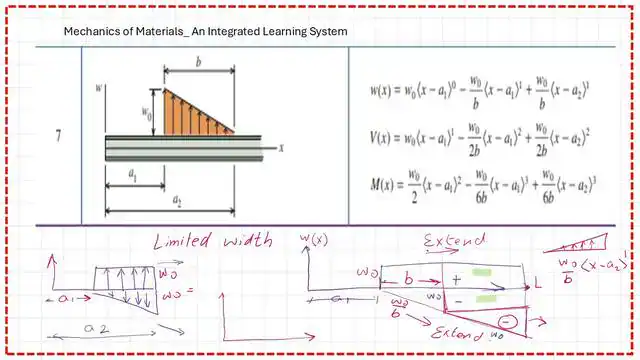
Part a) requires using the discontinuity function to write the expression for load w(x) in part a) and to include the beam reaction in the expression.
In part b), w(x) must be integrated twice to determine the V(x) and M(x).
In part c), it is necessary to use V(x) and M(x) to plot shear force and bending moment diagrams.
Find the beam reactions for Practice problem 7-38.
First, we draw the Free-body diagram for the beam, which includes two reaction forces. Ax and Ay at support A and one upward reaction force.
EY at support E is the ruler support. The total uniform load value is 800 multiplied by 7 equals 5600 lbs.
We have Ax and Ay for reactions; on the other support, we have a vertical load, EY.
This is a concentrated downward load of 3000 lbs and the concentrated moment of 8000 LB feet, acting anticlockwise and is a total load of the uniform load, as shown.
We have a positive direction from left to right for horizontal forces, and from below to up, it is considered positive for vertical loads.
While for moments, the anticlock direction is the positive direction.
If we start with the sum of X equal to 0, we cannot find any horizontal forces acting on the beam if we investigate it.
So we could say Ax=0.
We consider the sum of ∑Y=0. We can assume Ay + Ey Equals (3000 lbs + 5600 lbs). Then, Ay and Ey will equal 3000 + 5600 = 8600 lbs.
The last equation of equilibrium is the sum of ∑M at E=0. for all the forces.
Considering the anticlockwise direction is positive, the AY multiplied by its arm will create a moment in that direction.
Since it’s a moment in the clockwise direction, we’ll consider it negative. The Ay value is +4750 lbs, meaning the assumed direction is correct. The vertical reaction Ey equals 3850 Lbs.
Write the two expressions for w(x) and V(x).
We will move to the next slide. In this practice problem, we have 3 cases, 1-2 and 5 in the discontinuity function tables.
Case one is the case of concentrated moment, which we have anticlockwise of 8000 lb.Ft.
Case number two is the concentrated load, including the reaction at A, the focused load acting after 5 feet, and the other at E.
While Case 5 is the partially loaded uniform load, we have partially loaded uniform load acting. After 9 feet from the left, support and limited width, which is 7 feet.
We have several regions. We have one region from zero to five feet, followed by another area.
From 5 feet to 9 feet, then from 9 feet to 16 feet, and later from 16 to 20 feet.
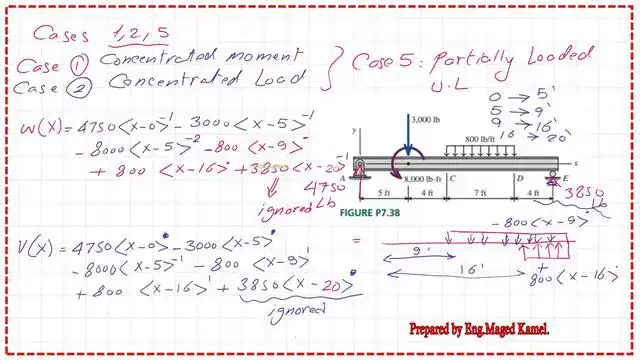
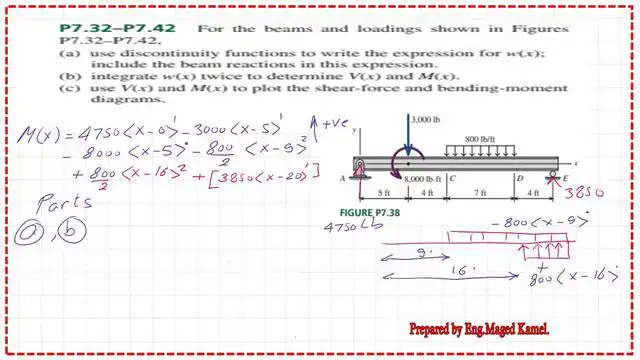
We start to write the load intensity W(x) equals. The first reaction is 4750 lbs, acting upward in the positive direction.
We’ll write 4750 multiplied by(x-0)^-1 and deduct the downward load, writing -3000 lbs *(x-5)^-1. We will extend the distributed load of 800 lb/ft to the end and add an upward distributed load of 800lb/ft with a length of 4 feet.
For the extended load. We write -800 * (x-9)^X ^0 +800* (x-16)^0.
Finally, the reaction of the right support, which is 3850 * (x-20)^-1, will be ignored in the Calculation since this will start to work for more than 20 feet.
We integrate once to get the expression for v(x). The full detailed expression is shown in the next slide image.
The moment expression M(x).
In the next slide, we continue to integrate, and we have the expression of M(x) equals 4750 * (x-0)^1- 3000 *(x-5) ^1, -8000 * (x-5)^0- (800 / 2) *(x-9)^2+800 / 2 * (x-16)^2+3850 * (x-20)^1. The last term will be ignored. Thus, we have completed parts A and B.
The shear values are based on V(x) from x=0 to x=11 Ft.
Part C will use V(x) and M(x) to draw and plot shear-force and bending moment diagrams.
In the next slide, we’ll introduce the expression of V(x) and start to get the values Of the shear at various points.
We start with V(x=0). We consider it as 0 plus or a small amount more than 0. We have the V(x=0 plus), which will be 4750 multiplied by.
Positive Value is to the power of 1; we consider it one. So V of X equal to 0 would be equal to 4750 lbs.
V of X of 3=4750 lbs. V of X of 5 equals 4750 * 5 raised to the power of 0=4750 lbs.
V of X of 5 equals 4750 * 5 raised to the power of 0=4750 lbs.
V(X) of 7, 4750 * 7 raised to the power of 0= 4750 – 3000 by 2^0=1750 lbs.
V(X) of 9, 4750 * 9 raised to the power of 0= 4750 – 3000 by 4^0=1750 lbs.
V(X) of 10, 4750 * 10 raised to the power of 0= 4750 – 3000 by 5^0-800*1=950 lbs.
V(X) of 11, 4750 * 11 raised to the power of 0= 4750 – 3000 by 6^0-800*1=150 lbs.
We will notice that there is an 800-lb drop. We are interested in the maximum moment or zero shear point. We assume that this point will occur between 9 and 16. So, we will write V(X ) =Zero.
The equation will be 4750*1-3000-800(x-9)=0. We have 800 * (x-9) = 4750 -3000, which gives 1750. We adjust the term and get the maximum value of X, which is 11.1875 feet.
This X is > than 9, but smaller than 16 feet.
The shear values are based on V(x) from x=12 to x=20 Ft.
We want to get the values from X equal to 12 to X equal to 20. V(X) of 12, 4750 * 12^0= 4750 – 3000 by 7^0-800*3=-650 lbs. V(X) of 15, 4750 * 15^0= 4750 – 3000 by 10^0-800*6=-3050 lbs.
V(X) of 16, 4750 * 16^0= 4750 – 3000 by 11^0-800*7=-3850 lbs. V(X) of 18, 4750 * 18^0= 4750 – 3000 by 13^0-800*9+800*2=-3850 lbs.
V(X) of 20, 4750 * 20^0= 4750 – 3000 by 15^0-800*11+800*4=-3850 lbs. This is precisely the numerical Value of the reaction at support E, which we have already calculated.
Values for M(x) for x=0 to x=11 Feet.
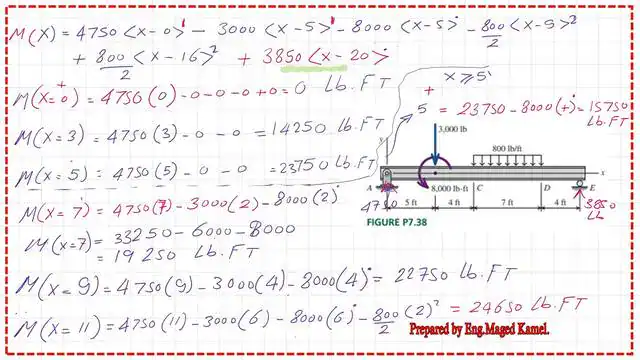
In the next slide, we want to get the expression of All the values for the moment at several points starting from zero until X is equal to 11. M(X) =4750*<x-0>^1- 3000*<x-5>^1-8000*<x-5>^0 -400*<x-9>^2+400*<x-16>^2+38/50*<x-20>^0.The last term will be ignored.
The Value of M(X) of 0 equals 4750*0=0 lb.Ft. The Value of M(X) of 3 equals 4750*3=14250 lb.Ft.
The Value of M(X) of 5 equals 4750*5=23750 lb.Ft. The Value of M(X) of 7 equals 4750*7-3000*2-8000*1=19250 lb.Ft. The Value of M(X) of 9 equals 4750*9-3000*4-8000*1=22750 lb.Ft. The Value of M(X) of 11 equals 4750*11-3000*6-8000*1-400*2^2=24750 lb.Ft.
Values for M(x) for x=12 to x=20 Feet.
In the next slide, we estimate the moment value for the points from X=12 feet to X=20 feet.
The first region is from zero to 5, the second region moves from 5 feet to 9 feet, and then we start from 9 to 16. The Value of M(X) of 12 equals 4750*12-3000*7-8000*1-400*3^2=24400 lb.Ft. The Value of M(X) of 14 equals 4750*14-3000*9-8000*1-400*5^2=21500 lb.Ft.
The Value of M(X) of 16 equals 4750*16-3000*11-8000*1-400*7^2=15400 lb.Ft. All values so far as positive will continue to be positive. The Value of M(X) of 18 equals 4750*18-3000*13-8000*1-400*9^2+400*2^2=7700 lb.Ft.
The Value of M(X) of 20 equals 4750*20-3000*15-8000*1-400*11^2+400*4^2=0 lb.Ft.
This is the end of Part 1 of Practice problem-7-38 Discontinuity Functions. Please refer to the second part of this post.
The previous post is the 4a-Part 2 of Practice problem-7-35 Discontinuity Functions.
There is a video for this post; this is the link.
This is a link to my “