Last Updated on April 14, 2025 by Maged kamel
Solved Problems For the Net Area Estimation.
This is an explanation in detail of the content of the subject.
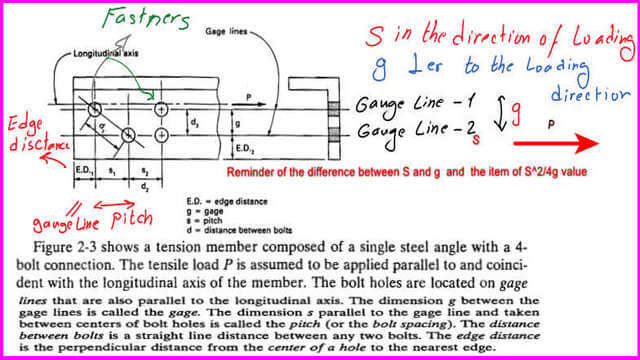
The next slide reviews the gauge lines, showing the first gauge line and the second gauge line in the direction of the force. The vertical distance between the gauge lines is g, and the distance between the centerlines of bolts is S, which is called the pitch.
The first solved Problem 3-4-2 for the net area estimate of a given angle.
We have two solved problems. The first solved problem, 3-4-2, requires estimating the net area for an unequal angle of 6x4x1/2″, where 15/16″ holes are used.
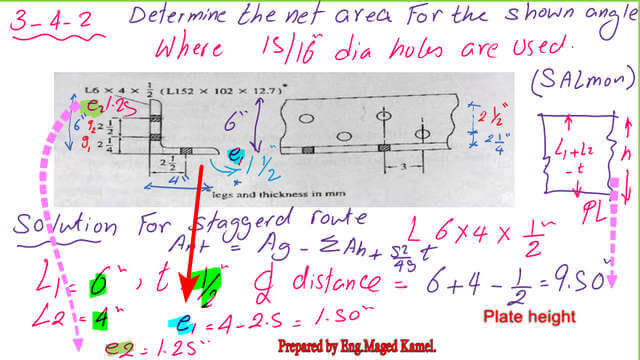
For the leg 6″, we have two gauge lines spaced horizontally by s-3″, and g distance =2 1/2″, while g edge distance=2 1/4″.To estimate the net area, we take the following steps:
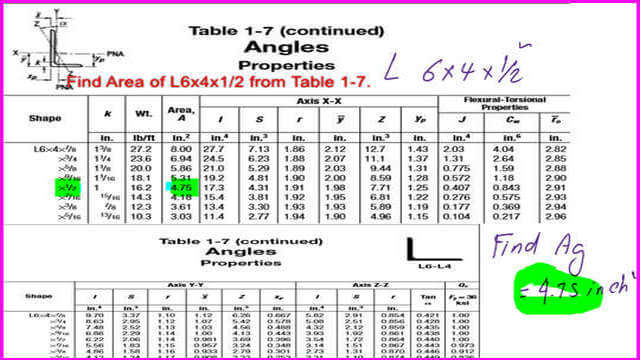
We have to get the gross area from Table 1-7 for our angle 6x4x1/2″, Ag=4.75 inch2.
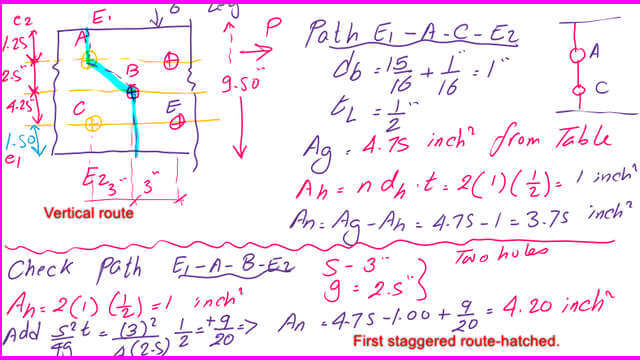
The edge distance g for AB is 2.50″, while the g distance for BC is 2.25+2.50-(1/4+1/4)=4.25″ since we are deducting the thickness of the angle.
A-check the different path lines and deduct the hole diameter *t, D is 1″ & t=1/2″. The angle will be unfolded to evaluate -g distances based on the centerline distances to the edge, as shown in the picture.
For path 1ACE2, we have two holes of D=1″, t=1/2″, then Anet=Agross- sum(d*t), Anet= 4.75-2*(1″)*1/2″=3.75 inch2.
B—For path E1ABE2, we have a zig-zag line Ab; we have to add (t*S2/4 g), where S = 3″ and g=2 1/2″; then, for the two holes of D=1″, t=1/2″. Anet=Agross- sum(d*t)+S^2/4g, Anet= 4.75-2*(1″)*1/2″+1/2*(3)^2/(4*2.50)=4.20 inch2.
C-check path E1ABEE2: We have three D=1″ and t=1/2″ holes. We have two zigzag lines with different g distances but the same S distance.
So we have to add (t*s^2/4*g1)+ (t*s^2/4*g2), then Anet=Agross- sum(d*t)+(t*s^2/4*g1)+ (t*s^2/4*g2).
Anet= 4.75-3*(1″)*1/2″+(1/2*(3^2/(4*2.50)+(1/2*(3^2/(4*4.25)= 4.75-1.5+0.715=3.96 inch2.
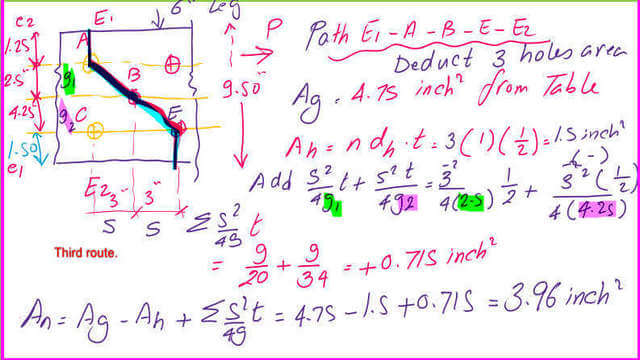
D-check path E1ABCE2: We have three holes of D=1″ and t=1/2″ and two zigzag lines, but each has different g distances.
But with the same S distance, we must add (t*s^2/4*g1)+ (t*s^2/4*g2). Anet=Agross- sum(d*t)+(t*s^2/4*g1)+ (t*s^2/4*g2), Anet= 4.75-3*(1″)*1/2″+(1/2*(3^2/(4*2.50)+(1/2*(3^2/(4*4.50)= 3.96 inch2.
The selected path is path ac for the net area Anet=3.75 inch2, with the most minor area for the solved problem 3- 4-2.

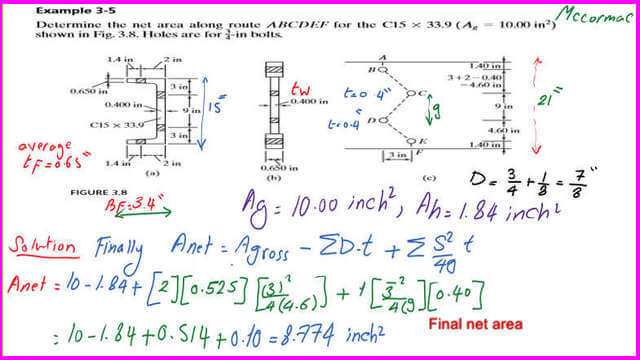
A Solved problem 3-5 for the estimate of net area for C channel.
In Solved Problems 3-5, the net area for channel C15x 33.90, which has four bolts with a diameter of 3/4 inch, must be estimated.
1-The C channel is to be unfolded. We will deduct 2tw thickness from the sum of its external dimensions.
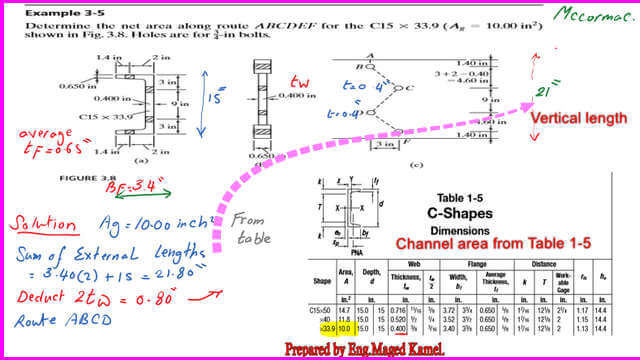
2- Get the area of the channel from the relevant table 1-5, Agross=10.00 inch2.
The I shape consists of two thickened portions for the flange, with width=tf-tw=3″ and thickness equal to 0.65″.
The middle portion is the web with a height of 15 inches and a width equal to 0.40 inches.
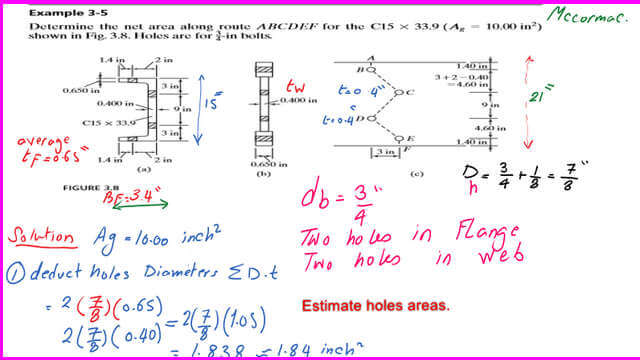
I have drawn the elevation of the I shape, which has four gauge lines. The vertical distance between the second and third gauge is 9″. The Other gauge distances are calculated by subtracting 9 inches from the overall depth and dividing by 2.
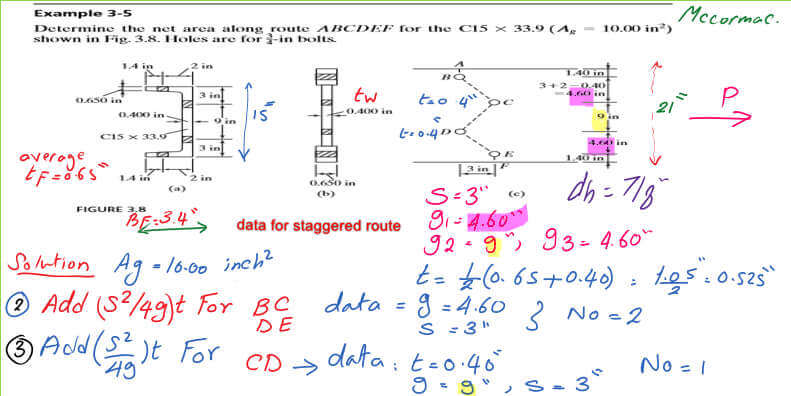
A—Examine the route ABCDE; for the solved problem 4-2, we have one zigzag line BC with S = 3″ and g=3+2-1*tweb=5-0.40=4.60″ and a second zigzag line CD with S = 3″ and g=9″.
The third zigzag line DE has s = 3″ and g=4.60″.3—four holes to be deducted with D=7/8″. There are two holes at the flange, with flange thickness=0.65″.
The other two holes are located at the web, where the web thickness=0.40″.
We can estimate the whole area to be deducted as 2*(7/8)*(0.65+0.40)=1.84 inch2.
We can estimate the ( t*S^2/4g) terms for lines BC, CD, and DE for the solved problem 3-5, as follows:
Since BC and DE are identical, the thickness is taken as the average of (0.65)+(0.40). Since the two lines pass through the flange and the channel’s web, the tav=1.05/2=0.525″.
While the CD route passes entirely through the web, for which the thickness is to be taken as t=0.40″. The final net area is equal to 8.78 inch2.
Practice Quiz.
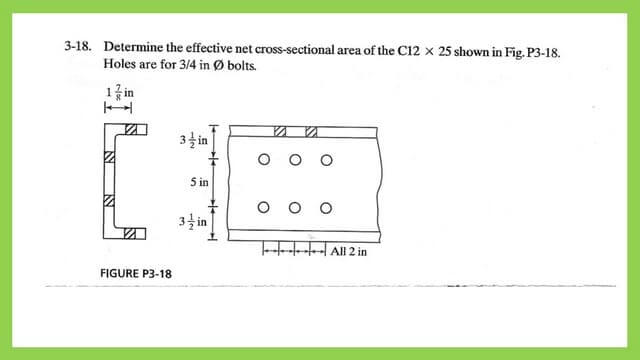
#1. Determine the effective cross-sectional area of the C12x25 shown in figure P3-18.
This is not the correct answer.
This is the following post: The Definition of the Effective Area for Tension Members.
Chapter 3 – Tension Members– A Beginner’s Guide to Structural Engineering is a great external resource.