How to determine the y bar for a right angle-case -1?
For more information about the difference between case-1 and case-2, please refer to post-2.
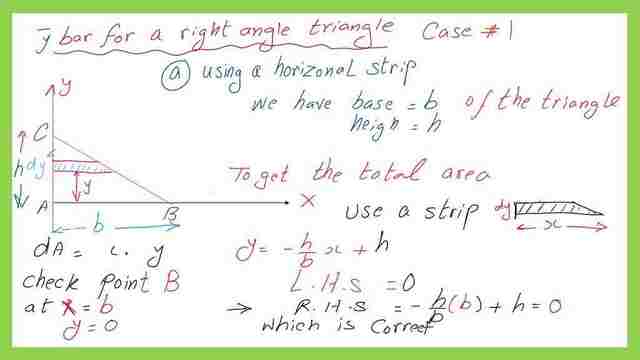
Using a horizontal strip to get y bar for a right angle- case-1.
We will start by using a horizontal strip to get the value of the y bar or the Cg vertical distance to the y-axis.
We have X and Y axes respectively and the base of the triangle. We have line AB with the length of b, the rise of the triangle is=h, and the inclined portion AC, equation: y =mx+C m which is a slope equal to -h/b *x, and the intersection with y-axis =h. The area of the strip is the product of (dy*x).
That’s why the AC equation is Y =-( h/b) *x+h. our horizontal strip breadth=x and the width=dy.
First, it is good to examine the equation of the inclined line BC By substituting the value of x=0 which is point C and check that the corresponding y value=h, when using the equation y=-(h/b)x+h).
We have Y=h when x=0.
For the second point which is point B, x=b, based on the line equation, the corresponding y value=0.
Perform integration for the horizontal strip to get the area of the right-angle triangle.
The area of the triangle is the summation of all the tiny horizontal strips, which can be expressed by using the integration for the strip from the start which is y=0 to the end which is y=h, considering moving the strip in the vertical direction.
Since the strip width is x and its height y from the x-axis. We are going to use the relation by y and x as derived from the equation of line BC. We will estimate the area dA as the product of xdy, since integration is in the vertical direction, we will omit x expression by substituting its value in terms of y.
The value of x derived from the line equation can be set equal to (h-y)/h*(b).
Proceed with the integration in the vertical direction starting from y=0 to y=h, we will get the final area=0.50*b*h, which is a known formula for the area of a right-angle triangle, that is the product of half base* height, where base equals b and height, equals h.
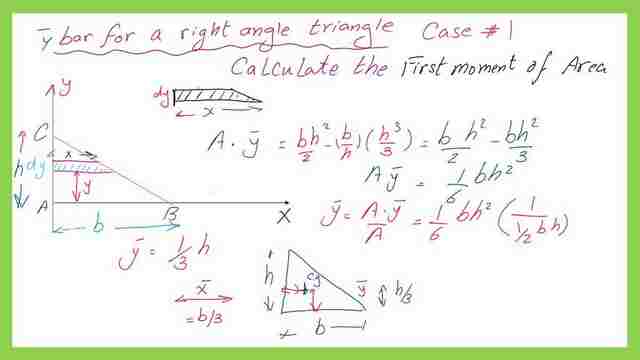
Integerate for the horizontal strip to get the first-moment area and y bar for a right angle triangle-case -1.
The expression of the first moment of the strip about the x-axis can be written as dA*y-strip, where the strip area is dA and y distance for the strip is the vertical distance from the Cg of the strip to the x-axis.
The expression of dA*y-strip is shown in the next slide image and integration will be carried out in the vertical direction from y=0 to y=h.
The final A*y bar represents the product of total area * the vertical CG distance from the X-axis will be found as in our case=b*h^2/6, where b is the triangle base while h is the height. The vertical distance between the Cg to X-axis which is designated as Y bar value will be obtained by simply dividing the first moment of area /Area. We will get y bar for a right angle=h/3 or one-third of the opposite side height.
The data for the X bar and y bar for the right-angle triangle is shown in the next slide image.
This is the link to view or download the pdf used for the illustration of this post.
For a good external reference, please refer to the following link.
The next post is X bar for a right angle-case-1-using vertical strip.