Last Updated on December 31, 2025 by Maged kamel
- Moment Of Inertia Iy for the rectangular section.
- FE reference manual tables for the area and moment of inertia for the Rectangular section.
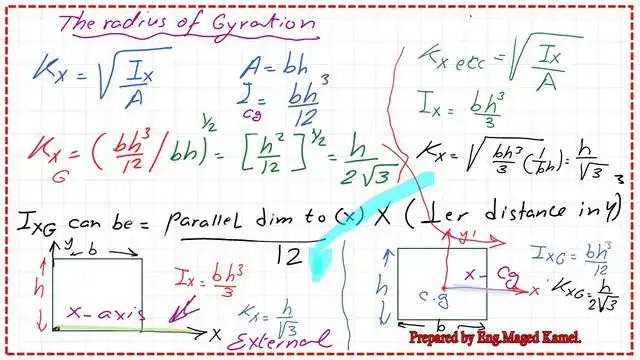
- How do we get kx, the radius of gyration for the rectangular section at x?
- How do we get the moment of inertia Iy for the rectangular section?
- A- using a vertical strip.
- The first method to estimate Iy for the rectangular section at the Cg.
- Another alternative method, or direct method, for Iy at CG.
Moment Of Inertia Iy for the rectangular section.
FE reference manual tables for the area and moment of inertia for the Rectangular section.
The first four items quoted from the NCEEs reference manual 9.5 are for the shapes of a right-angle triangle, represented by two cases: a triangle shape and the last case is for a rectangle.

How do we get kx, the radius of gyration for the rectangular section at x?
1-If we want to get k^2x at the external axis passing by the base, we will divide the
Ix value, which is( b*h^3/3/Area), then we will getk^2x=h^2/3. 2- But if we want to get k^2x at the axis passing by the center of gravity, by the base, we will divide the Ixg value, which is (b*h^3/12/Area), then we will get k^2xg=h^2/12.
How do we get the moment of inertia Iy for the rectangular section?
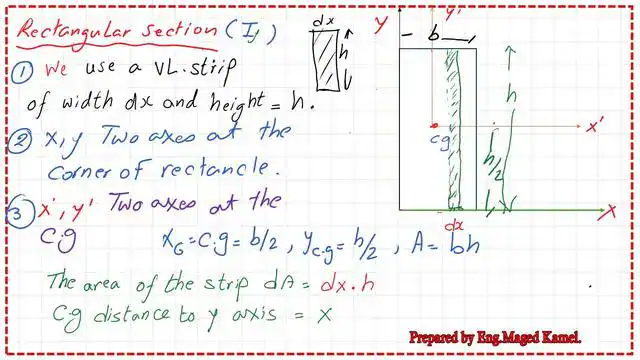
A- using a vertical strip.
The next step is how to estimate the moment of inertia About y. The moment of inertia Iy for the rectangular section at the y-axis passes by the external axis at the left corner.
1-The strip area =dx*h, and the horizontal distance from the CG of that strip to the vertical axis, y=x.
2-The moment of inertia for that strip =dIy=dA*x^2=h*dx*x^2.
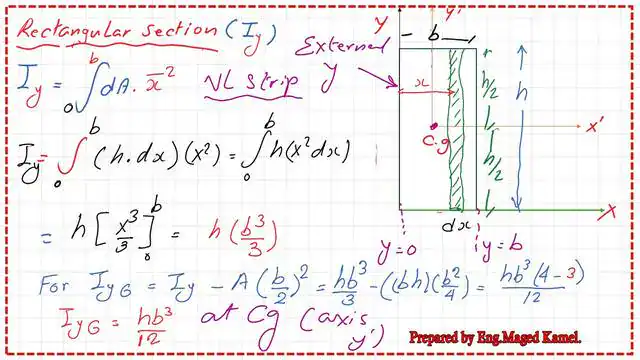
3-The moment of inertia for the whole section is the integration of the strip from x=0 to x=b, where b is the width of the section, while b is the section breadth. 4-The moment of inertia Iy for the rectangular section is =h*b^3/3 about the external axis-Y.
5-Iyg is the moment of inertia at the CG -hb^3/12, from the parallel axes theorem Iyg=Iy-(Area(x cg)^2=hb^3/3-(bhb^2/4)=bh^3/12. as shown in the next image.
A- using an infinitesimal area (dx*dy) .
The moment of inertia About y. For the moment of inertia, consider the rectangular section at the y-axis passing through the external axis at the left corner. We will use a double integral to calculate the infinitesimal area (dx dy).
1-The strip area =dx*dy, and the horizontal distance from the CG of that strip to the vertical axis- y=x.
2-The moment of inertia for that strip =dIy=dA*x^2=dy*dx*x^2.
3- We integrate from 0 to h for dy, then we integrate from x=0 to x=h.
4-The moment of inertia Iy for the rectangular section is =h*b^3/3 about the external axis-Y.
5-Iyg is the moment of inertia at the CG -hb^3/12, from the parallel axes theorem Iyg=Iy-(Area(x -cg)^2=hb^3/3-(bh)b^2/4)=bh^3/12. as shown in the next image.

The first method to estimate Iy for the rectangular section at the Cg.
1-Estimate the Iy about the external axis y which passes through the outer side of the rectangle, we have already estimated it as (h*b^3/3).
Iyg can be obtained by using the parallel axes theorem.

Another alternative method, or direct method, for Iy at CG.
There is another method to get the moment of inertia Iyg directly about the axis y’ passing by the Cg by producing a strip of (dx*h), the distance to y’ axis=x. The inertia of the CG is the integration of that strip from x =- b/2 to x = b/2.
Iyg for the rectangular section at the CG is h*b^3/12, the same as the value obtained in the previous calculation.

The radius of gyration Ky & kyg for the rectangular section.
Ky = sqrt (Iy/A), where Iy is Iy for the rectangular section since Iy = (bh^3/3) and A = bh. Since the numerator is under the sqrt, this h will go with h; one b goes with one b, leaving Sqrt(h^2/3).

K^2gy = IyG / A, Iyg = bh^3/12, and A = bh. Since the numerator is under the sqrt, this h will go with h; one b goes with one b, leaving Sqrt (b^2 /12).

You can download and review the content of this post through the following pdf file.
For an external resource on Engineering core courses: the moment of inertia.
The next post: How to get the product of inertia for a rectangle? This is a link to the Product of inertia Ixy for the rectangular section.