5- Easy approach for Product of inertia Ixy for a rectangle.

Last Updated on March 7, 2025 by Maged kamel

Product Of Inertia Ixy for a Rectangle at the CG.

The following post presents three methods to estimate the Ixy at the CG. 

The first method used to get the product of inertia Ixy for a Rectangle.

To get the Ixy at the CG for a rectangle, we consider the moment of inertia about the two axes passing by the CG.
1—The rectangle can be considered composed of 4 equal areas, like quarters; each quarter =A/4; for the first quarter, the x distance is at the left of the y’ axis, so the x distance is =-b/4, while the y1 is =h/4 with a positive sign. 

   2—We will check the signs of x&y for the remaining three quarters. For the second area, the xis+ve & y is +ve; for the third area, the xis-ve and y are also-ve. For the last quarter, the x-distance is -ve, and the y distance is also-ve.

3- Summing all the products of A_i *xi*y_i we will get Ixy at the Cg =0. The next slide image shows in detail the first method of estimation.

The second method to find the product of inertia Ixy for a Rectangle.

The second method to get the value of the product of inertia for the external edge and also at the Cg is as follows:
1-Introduce a strip of width dy and breadth=b.  
2- estimate the Ixy=∫h*dy*x/2*y from y=0 to y=h.    

3-the value of integration will be Ixy=Abh/4. 4 the value of Ixyg=Ixy-A(b/2)*(h/2)=0. the details are shown in the next slide image.       

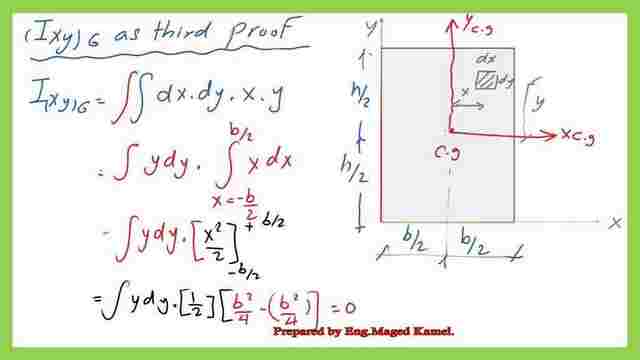
The third method to get the value of the product of inertia for the external edge and also at the Cg is as follows: 1-introduce a strip of width dy and breadth=dx.  

2-Ixyg=∬dx*dy*x*y, x, and y are the distances to the X-CG and Y-CG respectively, the integration will be done from x=-b/2 to x=b/2 and from y=-h/2 to y=h/2.   
3- The value of integration will be Ixyg=0.           

Ixy at the external axes.

Ixy at the external axes does not equal 0, but we will integrate the area (dAxy) from x=0 to x=b and from y=0 to y=h to get the product of inertia at the two axes at the external corner of the rectangle section.

This is a list of the data for the rectangle, starting from the first moment of area to the value of the product of inertia.

Polar moment of inertia.

The polar moment of inertia is Ix + Iy. If we want the polar moment of inertia value at the CG, we add both the moments of inertia at the CG, and we will get J0G=b*h(b2+h2)/12. At the external axes, the polar moment of inertia is j0=bh/3 (h2+b2).

This is the PDF used to illustrate this post.
For an external resource, engineering core courses, the moment of inertia.
This is a link to the next post, for the Moment of inertia.