Review of the Information of plastic bracing length Lp, Lr, Fcr.
How to estimate Lp?
Lp is the maximum un-braced length that will let the shape reach its plastic moment strength. The relevant equation for lp is introduced from Lp=300*ry/sqrt(Fy).
This equation gives Lp the bracing length at the plastic stage for any given section. we need to find out the radius of gyration at the y-direction, and the corresponding Fy or the yield stress for the section in question.


lp can be obtained if Fy=50 ksi from table 3-2 for the sorted w section by Zx.
How to estimate limiting laterally unbraced length Lr?
Lr is the limiting laterally unbraced length for the limit state. The relevant equation for limiting the laterally unbraced length for the limit state is shown in the next slide image.
Lr is the Limiting laterally unbraced length for the limit state. The general equation for the value of lr is included in the slide image.
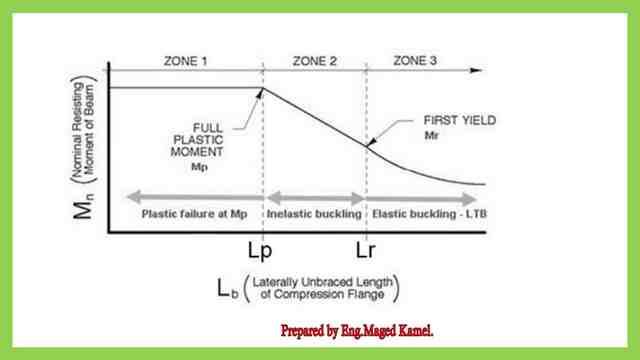
The next slide shows the different values of Mn or the nominal moment of a section based on the bracing length whether=Lp or between Lp and Lr or >Lr. based on these conditions we have three zones.


All requirements for this equation can be obtained from Table 1-1 for the W sections. Sx is the elastic section modulus at the x-direction, Fy is the yield stress, and E is the Modulus of elasticity.
Bracing length conditions.
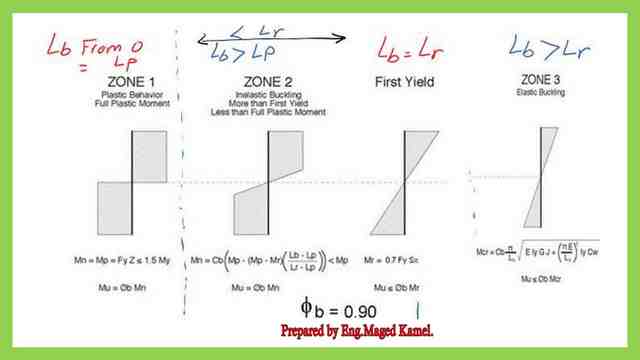

The next slide shows the equations used in the AISC to determine the value of a nominal moment for a steel beam, what is lb stands for?


The relation between Nominal moment Mn and bracing length Lb.
The next slide shows the three zones for the relation between the bracing length and the nominal moment of a steel beam.

Practice problem for Lp & Lr and Fcr.
It is required to find the bracing length at the plastic stage Lp and the limiting laterally un-braced length together with the value of Mp and Mr, for a given steel W24x176 at Fy=36 ksi. The steps will be as follows:
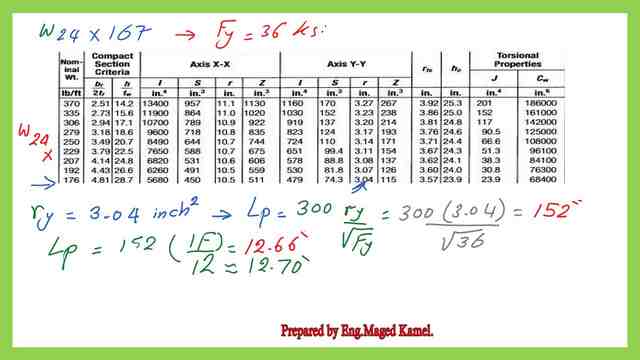
1-From AISC table 1-1 we get the values ry to get the Lp from the equation Lp=300*ry/sqrt Fy.
The value of ry can be found in AISC table 1-1 for the given section.
2-Substitute for Fy=36 ksi, ry=3.04 inch in the previous formula.


3- Apply in the formula of Lp=300*(3.04)/sqrt(36)=152″, we convert into feet by dividing /12.The value for Lp=12.70′ approximately.

How to get limiting laterally unbraced length for the limit state value?
1-if we refer to the next slide image, we know to estimate limiting laterally unbraced length for the limit state value. From AISC 1-1 we get the values ry, rts, Sx, ho, J, and consider C =1, these are the parameters for estimating limiting laterally unbraced length Lr for the limit state from formula F2-6.


The radius of gyration about y, ry=3.04 inch2,rts=3.57″ and the section modulus=450 inch3, ho=23.90″ n j polar=23.90 inch4, cw=68400.




2-Substitute for Fy=36 ksi, and all the needed items. The relevant calculation is shown in the coming slide image. The value for limiting laterally unbraced length for the limit state=49.01′




How to estimate Mp and Mr?
3- The calculations are shown in the next slide images. We can get the Mp, which is the plastic moment value, from the equation Mp=Fy*Zx, when We substitute in the equation Mp=Fy*Zx. The z value is 511 inch3, while fy=36 ksi.
We substitute and get the value of Mr=945.0. The value of Mp=1533.0 Ft.kips. We can get the Mr, which is the inelastic moment value, from the equation Mr=0.70FySx. The Sx is the statical section modulus for W24x176 and can be found to be=450 inch3.




How to estimate critical stress Fcr?
For a given bracing length Lb=50′, which is >Limiting laterally unbraced length for the limit state, we can find the value of Fcr by substituting it in the shown equation in the next slide image. The critical stress Fcr value is 24.60 KSI.


Using the following equation, Mrx =Fcr*Sx. When we substitute, we will get the value of Mrx=922.55 Ft.kips.
This is the pdf file used to illustrate this post.
For a useful external source, please follow this link. Lateral Torsional Buckling Limit State.
For the next post, Solved problem 4-6–how to get the available flexure beam strength?

