A Solved problem 5-1 for the elastic and plastic Moduli.
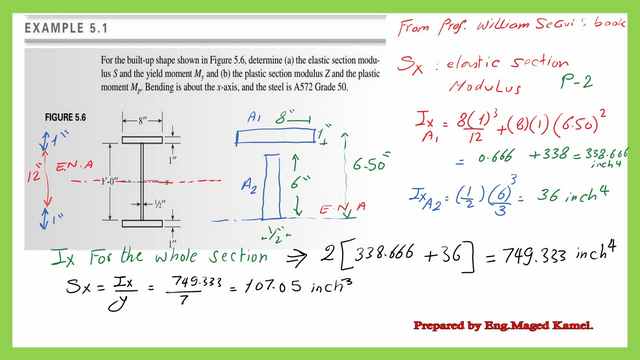
The first requirement is to get Sx=Ix/y, where Sx is the elastic section modulus, Ix is the moment of inertia about the x-axis, and y is the distance from the elastic neutral axis to the upper fiber, which is =Ix/y max.
We have converted the inner height of 1 ft =12″. For the Ymax=1/2(overall depth)=1/2(12+1+1)=7″.


Ix of the built-up section =sum of (Ix upper plate+Ix web+Ix of the lower plate); due to symmetry, it can be rewritten as Ix=2*(Ix-upper plate at the Cg+Ix -plate at CG). The Ix value =749.33 inch4; please refer to the next slide for more details of the calculations. Sx=Ix/y max, since Ix=749.333 inch4 and y max=7″, then Sx=749.333/7=107.05 inch3.

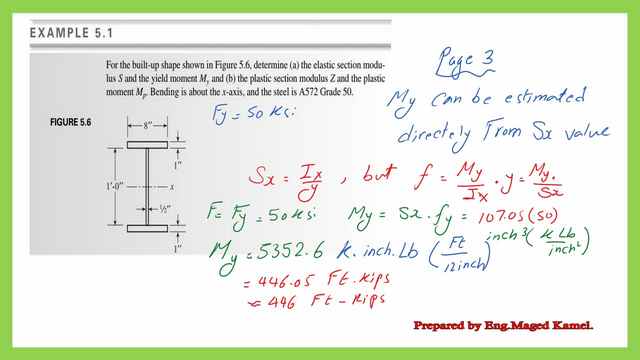
The second requirement is yield moment My which is My=Sx*Fy, based on the material of the steel section, is ASTMA572 grade 50, then Fy=50 ksi.
The yield moment My=107.0*50=5352.0 inch. kips, to convert to ft-kips, we will divide by/12. Finally the yield moment My=446 ft-kips, the details of the calculations are shown in the next slide image.

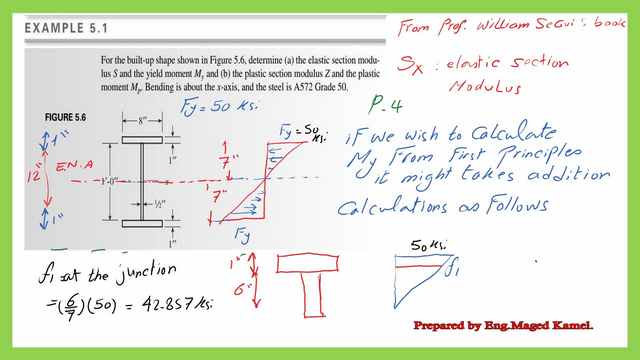
How to evaluate yield Moment My on a section by the first principles?
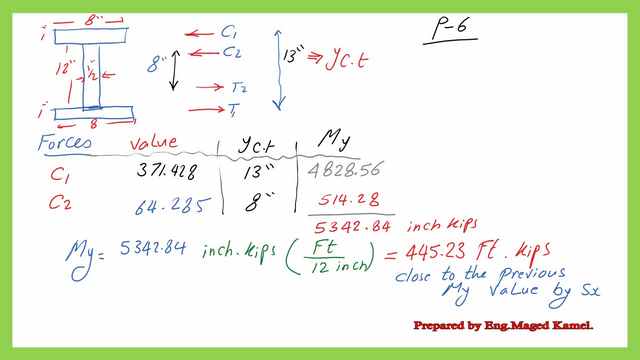
We can get the value of the yield moment My from the first principles by drawing a stress diagram, for which Fy=50 ksi, as shown in the next slide image. We equate the tension and compression forces as C=T=(1/2)Fy*(h/2), y ct is the arm distance between the compression force C and the tension Force T we call it yct=h-(2/6)h=2/3*h.

The compression force can be estimated as the sum of two compressive forces C1 and C2, where c1 is the force acting due to the trapezium stress distribution, While C2 is the force acting due to the triangular stress distribution portion. C1=371.428 Kips, while C2 value=64.285 kips. for each force, the distance of application from the neutral axis is shown in the following slide image.
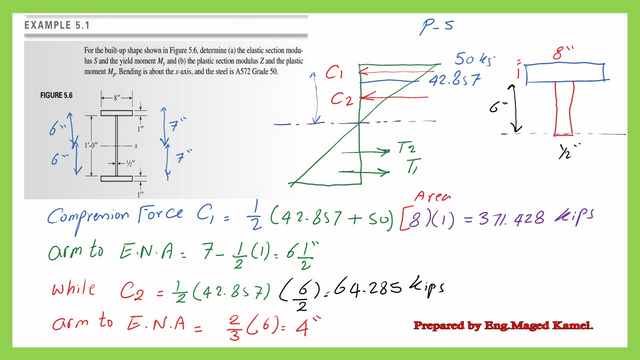

A tabulation of the compression forces and Tension forces is shown. C1 is the force acting on the Upper plate and C2 is the compression force acting on the middle web for a height of 8″. The corresponding tensile forces T1 and T2 are included. We can estimate the Yield moment value for the solved problem 5-1, by summing the two moments due to C1, T1, and C2 and T2 forces.

How to evaluate Zx for part b for the solved problem 5-1?
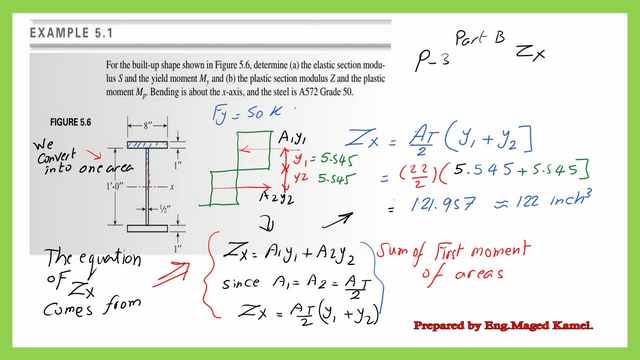
To evaluate the plastic section modulus Zx, we need to evaluate At/2, half of the total area, and find out the axis that divides the whole section equally. Due to the symmetry of the built-up section, we will get the P.N.A at 7″ from the bottom, thus coinciding with the elastic neutral axis, previously estimated.


We get the y bar for the At/2, half of the total area about the P.N.A, and estimate the value of the y bar, from the first moment area.


The plastic section modulus can be estimated as Zx=AT/2*(ybar1+y2), the full calculation is shown in the next slide.

How to evaluate Mp for part b of solved problem 5-1?
Mp=Zx*Fy, the plastic moment can be estimated as the product of Zx by the yield stress Fy.Zx=121.957 inch3, while Fy=50 ksi. The final estimated value is shown in the next slide. The Mp value for a solved problem 5-1 is 508.0 ft. kips.


This is the pdf file to illustrate this post.
For the buckling concept, please refer to this link from Prof T. Bart Quimby, P.E., Ph.D., F.ASCE site.
This is a link for the next post, Solved problem 5-2 for Sx&Zx and shape factor.

