Last Updated on November 9, 2025 by Maged kamel
Y bar for a right angle-case-1, using a vertical strip.
For more information about the difference between case-1 and case-2, please refer to post-2.
The following explanation will clarify how to calculate the y bar for a right angle-case-1 effectively.
Using a vertical strip to get the y bar for a right-angle angle-case-1.
For another approach, use a vertical strip to get the value of the y bar or the Cg vertical distance to the X-axis.
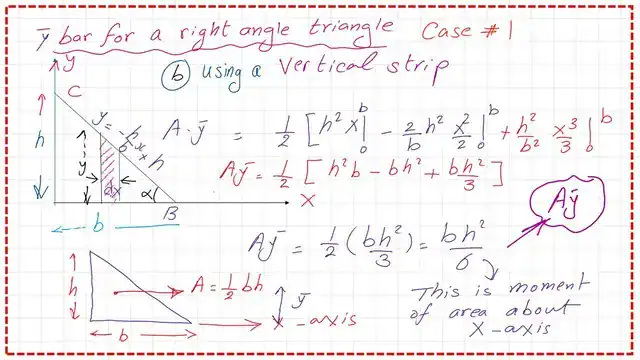
We have X and Y axes, respectively, and with a width equal to b. We have line AB with the length of b, the rise of the triangle is h, and the inclined portion AC, equation: y =mx+C, where m is the slope is equal to -h/b *x, and the intersection with the y-axis =h. The area of the strip is the product of (y*dx).

The width of the strip =dx, and its height is equal to Y. The strip area is equal to dA=y*dx.
Since we are integrating in the x-direction, we will omit the expression of y, by substituting its value in terms of x. The procedure is shown in the next image. The area=0.50*b*h, which is the same result obtained earlier by using the horizontal strip.
Perform integration for the vertical strip to get the area about the X-axis.
The expression of the dA*y-strip will be represented by the first moment of area about the x-axis, where y-strip is the horizontal distance from the Cg of the strip to the x-axis. The expression of dA*y-strip is shown in the next slide image, and integration will be carried out in the horizontal direction from x=0 to x=b. The details of the integration are shown in the next slide image.

Perform integration for the vertical strip to get the first-moment area about the X-axis.
For the Y bar for a right angle-case-1-using vertical strip, the expression of the first moment of area or the small strip about the x-axis is written as (dA*y), where dA=(y*dx), we utilize the expression of the equation of the line CB as y= -b/c*x+h.

The final A*y bar represents the product of total area * the vertical CG distance from the X-axis will be found as in our case=b*h^2/6, where b is the triangle base while h is the height.
Y bar for a right-angle final step.
Y bar value for a right angle will be obtained by simply dividing the first moment of area by Area. We will get y bar for a right angle=h/3 or one-third of the opposite side height. The value of y bar is shown in the next slide image.

For a good external reference, please refer to the following link.
The next post is X bar for a right angle case-2.