Last Updated on April 22, 2025 by Maged kamel
Estimation of Max and Min-moment of Inertia For a Section.
Steps to get the expression for I-max and min-moment of inertia, and tan(2θ).
Our calculation for the bending of stress is based on the pure moment assumption as we will estimate the product of inertia Ixy to ensure that it is equal to zero.
The neutral axis, for which Ixy = 0, must pass through the Cg.
The principal axes for the two perpendicular axes should be number #2, meaning that Ixy should equal zero.
We must examine both of the orthogonal axes when we estimate Ixy and discover that it is not equal to zero, as this will result in Ixy=0.
Numerous axes can be used to obtain l-polar = Ix+Iy or = Ix1+Iy1 or Ix’+Iy’ because the value of I-polar is constant. However, the axes that will produce the moment of inertia are the ones that we have an interest in, for instance, x’ will produce the most moment of inertia and y’ will provide the smallest, and Ix’y’ should equal zero simultaneously.

If Ix is the maximum, Iy is the minimum, and Ixy is zero, then any two axes are classified as principal axes. The term “principal axes” refers to these two axes.
Derive the expression for max and min-moment Of Inertia.
Using the x and y axes, we will create a general expression and assume that we have two inclined axes, x’ and y’, with an angle of = θ, where θ is positive and pointing counterclockwise. To establish a relationship between (x’ and y’) and x and y, for small strip dA, the coordinates are X and Y equally referring to the new two axes (x’ and y’).

The formula for x’ is x*cos θ + y*sin θ. This part of the x’ is represented by y’=ycosδ -xsinδ.
Then, since we know that Ix’ = ∫ dA*y’^2, this is the dA, and we wish to make an integration about x’, we continue to calculate the moment of inertia about x’ and y’ while also attempting to obtain an equation for Ix’ and Iy’, for the special case where Max and Min-Moment of Inertia are needed. However, it will be = ∫ dAx’^2 for the moment of inertia surrounding y’. Conversely, for the inertia product Ix’y’,= ∫ dAx’y’.
The values of x’=xcos θ+ysin θ and y’=ycosδ -x*sinθ will be substituted. The following graphic shows we have Ix’, Iy’, and Ix’y’. These items are written after the values of x’ and y’ are substituted in terms of x and y.

To some extent, this calculation is lengthy, but our goal is to obtain three expressions. In terms of x, y, and angle θ—the angle closed between axis x and axis x’—the first expression is for Ix’.
In terms of x, y, and angle θ—the angle closed between axis x and axis x’—the second expression is for Iy’. Regarding x,y, the third expression is for Ix’y’, where θ is the enclosed angle between axis x and x’.

Since the polar of inertia is equal to Ix + Iy, the first two expressions for Ix’ and Iy are displayed in the next slide.
Once we sum up Ix and Iy from Ip, we can obtain the expression for tan(2θp).

We will add Ix and Iy together from Ip, we can get an expression for tan(2θp).
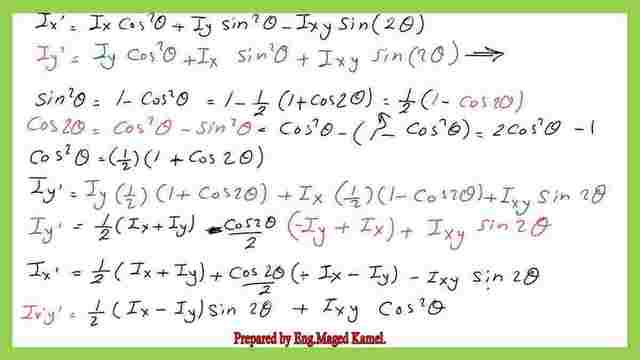
The angle θp, which produces Ix max and Iy min, can be obtained by differentiating Ix’ concerning θ and setting it equal to zero.

The expression for max and min-moment of inertia and principal angle θp.
The principal angle θp is the angle between the x-axis and the principal axis of inertia. We use twice the value of the principal angle in the NMohr circle of inertia.
The tan(2θp) is expressed as tan(2θp)=2(Ixy)/(Iy-Ix). As we recall this expression, we can change it to produce (-2Ixy/Ix-Iy) as a denominator, the θp. When we set θ as equal to θp, we can plug in the expressions for Ix’ and Iy’ and substitute by θp. Then we can get the Max and Min-Moment of Inertia expression. Please refer to the image on the next slide for more information.

The four cases for the relations between Ix, Iy, and Ixy.
We have obtained the enclosed angle, principal axis θp, between the X- and X’-axes, as we need it to formulate the tan2θ expression. Four cases are presented, the first being Ix>Iy, and Ixy is positive.

The second case is when Ix>Iy and Ixy are negative. The third case is when Ix < Iy and Ixy is positive. The fourth case is when Ix < Iy and Ixy is negative.
There is a video for the content of this post.
The following post is an Easy introduction to Mohr’s Circle of Inertia Part 1.
This links to a valuable external resource: a calculator for Cross Section, Mass, Axial and Polar Area Moment of Inertia, and Section Modulus.
