Last Updated on March 21, 2024 by Maged kamel
Introduction To Numerical Analysis Part 1.
Difference between Numerical and analytical methods.
Introduction to Numerical Analysis by using numerical methods, which are techniques by which mathematical problems are formulated to be solved with arithmetic operations again and again.

It is important as an introduction to numerical analysis to find the difference between Numerical and analytical methods and to understand what is a polynomial. Numerical methods provide an approximation to the problem in question, while the analytical method gives exact solutions with more time-consuming.

Numerical methods only give the solution at a certain point, like finite difference and finite element; these methods are considered Numerical since they give results at certain points.
Definition of the Quadratic function.
A quadratic function is a function that can be expressed in the form of f(x)=ax^2+bx+c. There are three cases to get real solutions. Depending on the relation between b^2 and 4ac. The complete illustration is shown in the next slide image.

Refer to this link for more information. What is discrimination? Therefore, the discriminant formula for the general quadratic equation is Discriminant, D = b2 – 4ac, Where
a is the coefficient of x2, b is the coefficient of x, and c is a constant term.
Definition of the polynomial function.
The polynomial function with degree n has a leading coefficient an and has a constant a0 and can be written as f(x)=anx^n+an-1*x^n-1+an-2*x^n-2+……..+a0.

Roots findings.
As an introduction to numerical analysis, we will review the concept of root-finding of a function. The roots of a function, or zeros, are the points where the function crosses the x-axis, where the value of f(x)=0; for analytical methods, we use synthetic division, and for quadratic functions, we use the following equation for the solution.
The remainder theorem.
The remainder theorem is a formula that is used to find the remainder when a polynomial is divided by a linear polynomial.

When a certain number of things are divided into groups with an equal number of things in each group, the number of leftover things is known as the remainder. It is something that “remains” after division. Let us learn the concept of the remainder theorem.
Roots for y=x^2-4.
If we have a graph. Y = x^2 – 4, we draw the x and Y coordinates while the intersection of the x-axis.
The graph will give us the value of f(x) = 0. Supposed to cross at +2 & -2. These two points are points of zero. How do we get these two points? we let f(x),or y=0 . We make bracketing (x^2-4 ), which will give us a multiplication of (x+2) *(x-2). We equate to zero, so( x= -2).
The first solution or there is another solution that x =+2. We have two solutions x = – 2 or x =+ 2, they are the Zeros? The second or last step is that we have to check that our solution is correct. x= +2, this equation y =x^2-4 ,we put x=+2 so y=2 to power of 2=4-4 ,gives us zero .
And for the other solution x=-2, we will write -2 ^ 2 – 4, which will give us zero. Once we have satisfied the f (x ), =0
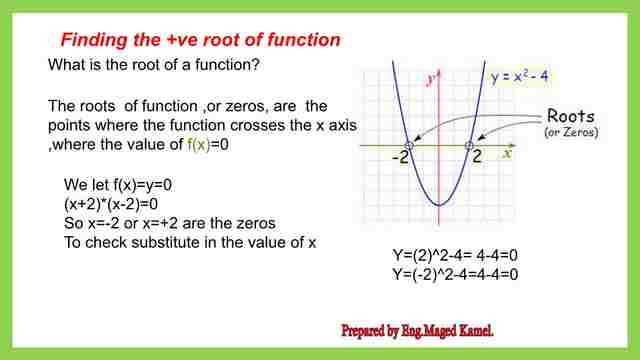
We have these two zeros, + 2, and -2. In synthetic division, to get the zero of the function sometimes, we are guessing the value of the X. with -the so-called rational roots. In the next slide image, a representation of a function y=x^2-4 is required to determine the roots of that function.
This is a graphical representation of the solution of the function, which means it has a root or more, if one root is shown in the graph one point is shown for the curve of the function touching the x-axis with y=f(x)=0.
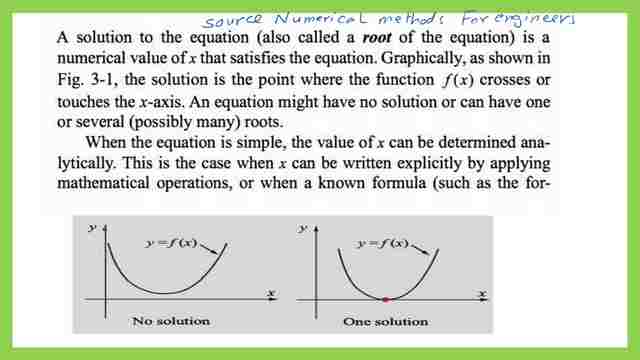
On the other hand, if there is no solution, then there will be no intersection of the function’s graph to the x-axis. This is a graphical representation of the solution of the function; the solution could be multiple points or only one point based on the number of intersections with the x-axis.

The next post is What is synthetic division? Numerical Analysis Part 2.
This is a link to download the PDF data used in the illustration.

