What is synthetic division? Numerical Analysis-part 2
As an introduction to numerical analysis, we will review synthetic division. Synthetic division is a shorthand, or shortcut, method of polynomial division in the special case of dividing by a linear factor and it only works in this case.



Synthetic division is generally used not for dividing out factors but for finding zeroes (or roots) of polynomials.
In synthetic division, to get the zero of the function sometimes, we are guessing the value of the X. with -the so Called Rational roots. The rational Root is a handy way of obtaining a list of first guesses when you are trying to find the Zeros of the polynomial.
A Solved problem #1- for synthetic division.
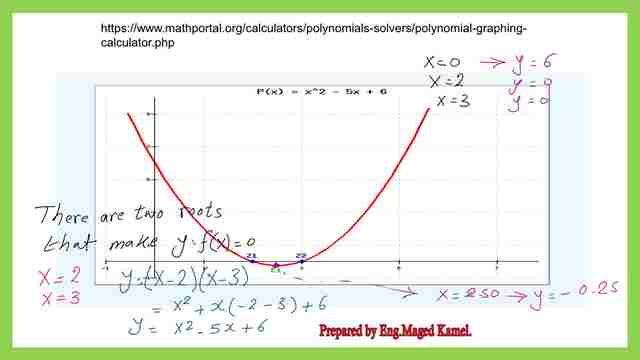
In our example. Y = x ^2 – 5 x + 6. We have a leading coefficient of x^2 = +1. This one can be analyzed at the multiplication (+1*+1)=1, and( -1*-1 )will give us 1, while the 6, the constant, can be analyzed. as either (1*6) or(-1*-6) or (+2*+3) or (-2*-3).
So we have 1, and 6 + and – will put it here.
And for the leading coefficient, we have 1 and 1 + and -(1*1),(-1*-1).
We put it down here in the denominator and comma; plus or minus, we have 3 either plus or minus divided by the leading coefficient. Now we will Proceed to make the synthetic division. We are writing the coefficients only without the x^2 or x, for x^2. The coefficient of x^2 is 1.
We put (+1*+6),(-1*-6),(+2*3),(-2*-3).The first guess is (x+3)=0 for the first time. X will be = – 3, will go there. We Put this – 3 here at the left side portion. The coefficient of x ^2 or the first coefficient. It will go down as 1.



Then we multiply one by -3; we put it here we add -5 to -3, we get -8, then we multiply -3 by -8. -8 multiplied -3, we get + 24, which we put here, and we add 24+6. We get + 30; as long as we do not get the zero, this point is not a root point, then we proceed with guessing another value. So these are the steps.
1-Our next guess is (x-2)=0; the coefficient of x ^2 will be carried down, multiplied by (+2), then add -+5 to add to +2, and we will get -3.
2-(-3) to be carried down, again multiply by(+2), we will have (-6), add to +6, we get a zero, this means that (x-2) is a zero point. Our solution x- 2 is one of the solutions.
3- we utilize (x-3), the next guess is (x-3), we use +3, 1 will go down, multiply (+13)=3, add to (-3), we get zero value.
4- the two roots are (x-2) and (x -3 ). Now multiply by each other, and you will have (x^2-5x+6) as the same function y=(x^2-5*x+6).


The next slide image shows the graphical solution of the previous function by tabulating different values of x and estimating the corresponding y value.

A solved problem for a synthetic division with a remainder.
The next slide image shows the division of f(x)=x^3-2x^2+x-3 by(x-2) using synthetic division. There will be a remainder of (-1).


A Solved problem for dividing a given function by a value.
Our new function is
1- It is required to divide the function by(x+2).
2- We have the following coefficients: for x^5 is 4, for x^4=0, for x^3=+6, for x^2=-9, for the constant is +6
3- We start with the solution of (x+2)=0; we divide by (-2).
4- number 5 will continue down, multiplied by -2, the product which is -10 will be placed as a second item and added to +6, the value will be -4.


5- (-4) to be multiplied by -2, the product which is=+8, to be placed as a third item.
6- Add +8to(-9), and the value which is -1 to be placed down.
We proceed to step 8, as shown in the next slide image.


Since we have no zero value, there will be a remainder which is expressed as shown in the next slide image.


A Solved problem for dividing a given function by a value-long division.
The same problem will be solved by using the long division procedure; instead of putting (-2), we will use(x+2).


The values of 5x^4+6x^3-9x^2-7x+6 will be written on the right side of the (x+2). Divide 5x^4/x=5x^3.
Multiply(5x^3)*(x+2)=5x^4+10x^3. Subtract this value from (5x^4+6x^3). The result will be -4x^3.
Divide -4x^3/x=-4x^2.
Multiply(-4x^2)*(x+2)=-4x^3-8x^2.+10x^3. Subtract this value from (-4x^3-9x^2. The result will be -x^2.


Divide -x^2/x=-x.


Multiply(-x)*(x+2)=-x^2-2x. Subtract this value from (-x^2-7x+6. The result will be -5x+6.


Divide -5x /x=-5. Multiply( -5 )*(x+2)=-5x-10.


Subtract (-5x-10) from (-5x+6). The result will be 16. There will be a- remainder of 16/x+2. The full details are shown in the next slide image.


This is a link to download the PDF data used in the illustration.
The next post is about the Bisecting method, a numerical method for rooting findings.
A very intersection source is Holistic Numerical methods.

