Solutions for Block Shear-Coped Beam Problem.
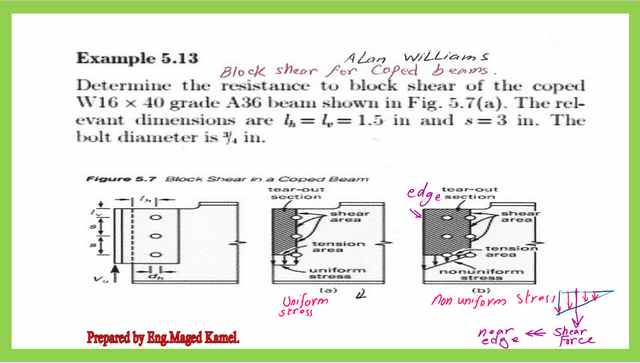
In this post, we will introduce solutions for the Block Shear-Coped Beam Problem. A solved problem is quoted from solved problem #5.13 from Prof. Alan Williams‘s handbook.
The solved problem shows how to estimate the block shear-coped beam value when the factor for block shear UBS equals 1.00, which is the case where we have a uniform stress distribution for tension force.
A solved problem for Block Shear-Coped Beam-case-1-UBS=1.00.
It is required to determine the resistance to block shear of the coped beam W16x40 grade A36.
The horizontal distance between the beam edge and the center line of the first line of bolts is 1.50 inches, and the vertical distance between the edge of the beam to the first line of bolts is 1.5 inches.
The vertical spacing between bolts is 3- inches as shown in the next slide image. The bolt diameter is 3/4 inches.

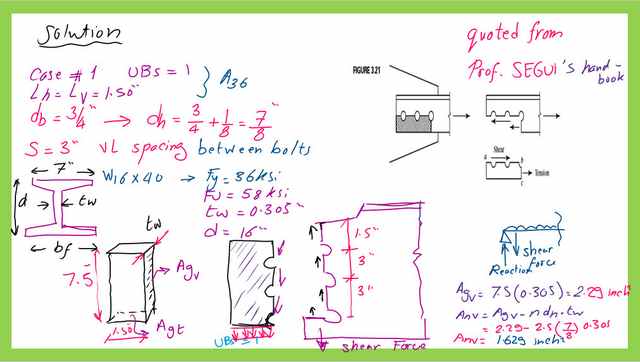
Gross and net area for shear-UBs=1.
- For W16x40, the web width is 0.305 inches, the breadth of the flange is 7 inches, and the flange width is 0.505 inches. The yield stress for A36 is 36 ksi, while the ultimate stress is 58 ksi.
For the hole diameter, we add 1/8 of inches to the bolt diameter and the hole diameter will be equal to 7/8 inches.
2-There is one section that is subjected to shear, and that is the vertical section through bolts. There is also one section that is subjected to tension, and that is the lower section.
3-We estimate the gross area for the vertical section subjected to shear which can be found equal to =(7.50×0.305)=2.29 inch2. To get the net area for shear or Anv we deduct the area for two holes and a half, the net area Anv can be found equal to 1.625 inch2.

Case of shear yielding and tension rupture.
In the slide, we can see the case of shear yielding, where we have Agv equals 2.288 inch2. The acting shear stress is equal to 0.6*Fy, Since Fy=36 ksi. The shear stress accordingly will be equal to (0.6*36)=21.6 ksi.
Multiply the shear stress by the gross area for shear to get the shear yielding, which will be equal to 49.42 kips.
For the case of tension rupture, first estimate the gross tension area equal to width by web thickness or (1.5*0.305)=0.458 inch2. To get the value of the net area for tension, which we call Ant, we will deduct one hole diameter area. As we can see from the slide, the Ant will be equal to 0.3241 inch2. The Ubs value equals 1. The ultimate stress Fult=58 ksi.


Case of shear rupture and tension rupture.
For the case of the shear rupture and tension rupture-LRFD., the block shear-coped beam Phi value equals 0.75, we will multiply (0.60*Fult*Anv) plus (Ubs*Ant*Ful) by the Phi value. The result can be found to be equal to 56.46 kips as shown in the next slide image.
We will select the min value of (51.20,56.42) which can be found equal to 51.20 kips, which is the LRFD value for block shear-coped beam for UBS=1.
For the ASD value, we can find that for the case of shear yielding and tension rupture it is equal to 34.13 kips, while for the case of shear rupture and tension rupture it is equal to 37.64 kips, we will select the minimum value which is kips for UBS=1.


Estimate the final LRFD value for block shear.
Now we are ready to proceed to our estimation for block shear. We have a yield stress of 36 ksi and an ultimate stress of 58 ksi. The gross area for shear, Agv equals 2.228 inch2. The net area for shear is equal to 0.3241 inch2.
The first case is the case of shear yielding and tension rupture. For that case, the shear stress is equal to (0.60*Fy), while the tension stress is fult acting on the net area of tension Ant. Please refer to the left side of the slide.
Shear yielding is estimated as equal to 49.42 kips. The tension rupture equals UBs by Fult by Ant, the UBS value equals 1, Ant equals 0.3241 inch2, and the Fult=58 kips. The total value of tension rupture will be equal to 18.798 kips. Adding the value of shear yielding and tension rupture will give a total value of 68.218 kips.
The second case is the case of shear rupture and tension rupture.
Please refer to the right side of the slide, for that case the shear stress is equal to (0.60*Fult), while the tensile stress is Fult acting on the net area of tension Ant. The shear rupture value equals 56.411 kips and the tensile rupture equals 187.798 kips.
Adding the value of shear rupture and tension rupture will give a total value of 75.028 kips.


If we want to find the LRFD value for block shear for the first case, we multiply phi, which is equal to 0.75, please refer to the left side of the slide, Phi will be multiplied by opening a bracket (0.60Fy*Agv plus ( 0.60*fult)*ubs*Ant. The final LRFD value for case 1 equals 51.16 kips.
We will select the minimum values of the two values which are (51.20 and 56.46). The final LRFD value for Block Shear-Coped Beam will be equal to 51.20 kips.
That means shear yielding and tension rupture controls.
Estimate the final ASD value for block shear.
For the ASD value, consider (1/omega)=(1/2).
We can find that the final ASD value for the block shear*-coped beam will be equal to 34.13 kips. We have come to the end of the solved problem.


For more details regarding block shear, please refer to the post -*Quickstart to the introduction to block shear resistance.
Our next post will discuss how to use AISC tables to get the block shear, yielding, block shear rupture, and tension rupture values and how to develop these expressions. Please find the detailed post.
A new post: Post 21-Case 2 for the block Shear-Coped Beam Problem.
For an introduction to coped beams, please refer to the previous post, post 13-The relation between Block shear and coped beams.
For a more detailed illustration of block shear, there is a very useful external link-Tensile yielding and tensile rupture. A Beginner’s Guide to the Steel Construction Manual, 14th ed.

