Last Updated on July 18, 2025 by Maged kamel
A Review of Portal frames-pin supports at the base.
We stopped at the end of the previous post while discussing the approximate method for the portal frame. How to perform a structural analysis, and we provide an example: a frame with two hinged supports acted upon by a force at the left side.
The portal frame is analyzed in two frames.
The frame can be analyzed by dividing it into two parts: the first part has antisymmetrical loading, and the second part has symmetrical loading, resulting in elastic curvature.
We can assume that we have roller support in the middle of the girder. In the next slide, after creating roller support in the middle of the girder, we will examine the support reactions.
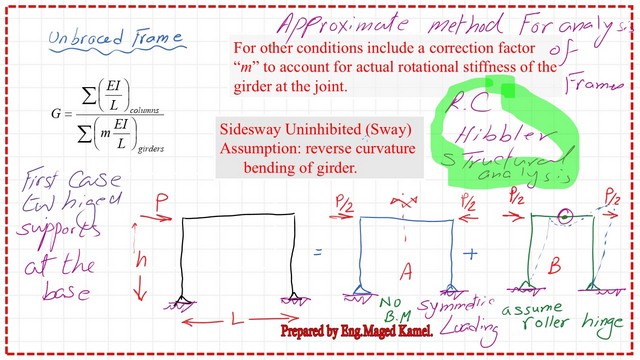
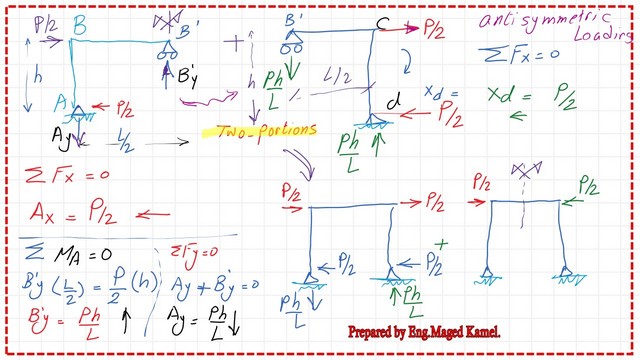
If we consider the portal frame height is h, the lower joint is A, the upper left corner is b, the right corner is c, and the last support is D.
Estimation of the portal frame reactions.
The roller support distance is at L/2, and this is the continuation of the frame. If we look at the left side portion, we have P/2 at the left side from left to right and another load P/2 at the right joint acting to the right from the sum of forces at the x-direction ∑Fx=0, ∑Fy=0, ∑M=0.
We can determine the magnitude of the reactions for the lower hinged support and also for the roller support at B’, since the hinge at A can take the horizontal force. Since the roller support at B’ can not take that force, Ax=P/2, so ∑Fx=0 is utilized.
The reaction Ax is to the left. Taking the bending moment at A =0, the Vertical reaction at B’ can be estimated as B’y*L/2=P/2*h, B’y=(P/2)*h/(L/2)=B’y=P*h/L=P*h/L, due to the summation for moment =0.
From ∑Fy=0, since there are no external forces in the Y direction, then Ay will be =b’y=P*h/L but acting downwards. At B, force B’y will act upwards. At the joint, on the right side, there will be a force= P*h/L acting downwards.
The reaction at d will be P*h/L acting upwards since we have a force at joint P/2 acting to the right, for ∑Fx=0, at support d, the joint force Xd=P/2, acting to the left.
We can get the reaction for the first part: the horizontal reaction at A is P/2, and at D, it is also P/2. The vertical reaction at A is Ph/L, downwards, and the vertical reaction at D is Ph/L, upwards. For the other frame, we have P/2 and P/2 as joint loads.
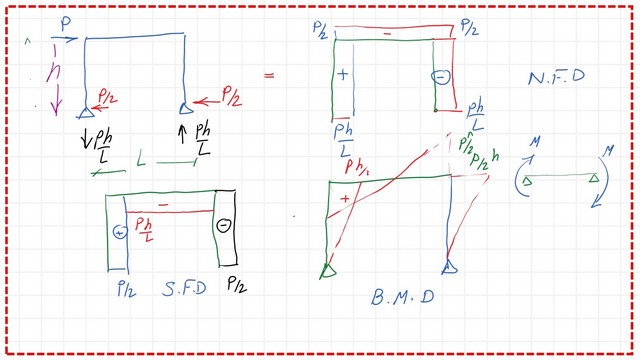
After summing the two frames, we can get the final situation, the normal force diagram, the shear force diagram, and the moment diagrams.
How to draw internal forces diagrams of the portal frame-pin supports at the base?
We have a tension force of p*h/L for column AB at joint B. The compression force for member bc will be (P-p/2)=p/2 acting at joint C. Then, we have a compression force, P*h/L, acting at joint D for member DC. That was a review of portal frames that have two-hinged support.
For the shear force at joint A, we have a positive force = P*h/L, which will act until the joint. The P*h/L acting anticlockwise will create a negative shear for member BC. From D to C, we have a negative shear force = P/2 until joint C.
For the bending moment diagram, we have a moment at joint b=P/2h, at the corner, there is a moment. At the middle moment, then continue to join C, the value is Ph/2.
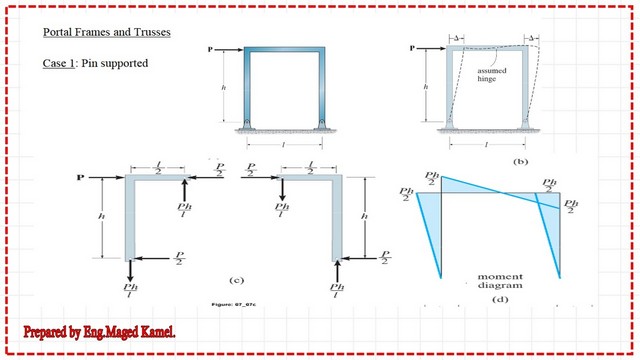
The value of m=0 at joint D will remind us of the double curvature, where we have two equal moments in the same direction. The same result is also shown in these diagrams, but I have explained in more detail that the bending moment diagram is drawn on the positive side.
This is a link to A very useful external link, Concentrically Loaded Compression Members.
This is the next post, Analysis of portal frame-fixed supports at base.