Last Updated on January 1, 2026 by Maged kamel
Product Of Inertia Ixy- For the Triangle.
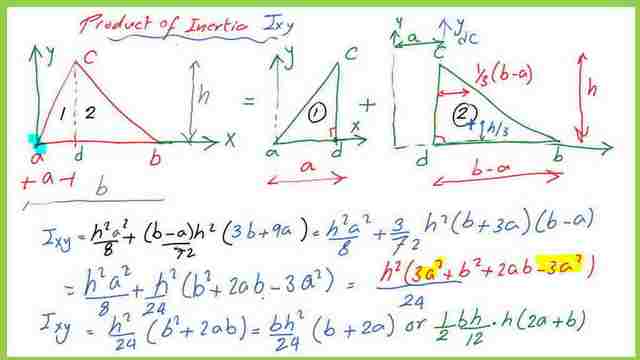
Product of inertia Ixy for the triangle.
We aim to determine the product of inertia Ixy for the triangle at the intersection of the x- and y-axes at point a.
We will use the previously obtained product of inertia from the earlier posts for both cases 1 and 2.
1-Since the triangle ABC consists of two triangles, ACD and dbc. Our Ixy for the triangle = Ixy1, precisely as estimated from case 2, but for case 1, the Ixy value needs to be adjusted since it is calculated at the ydc.
The adjustment is done by taking Ixy value at the CG of the triangle cdb and adding a new value for Ixy from the CG to the new y-axis at Point a. The value is estimated as the triangular Area of case-1*x1^2 to be added. x1 is the Cg distance to the Y-axis. xcg =(1/3*(a+b)), the y- cg =h/3. The matching items should be cleared, and the product of inertia Ixy estimation in detail is shown in the next slides.
Omit(+ 3a^2) with the (-3a^2), and proceed to the calculation for the product of inertia Ixy for the triangle.
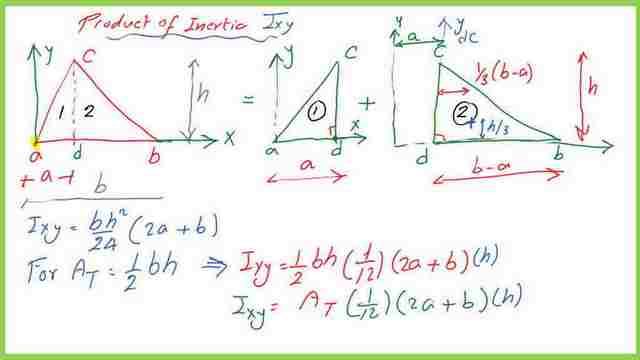
The value of Ixy relative to the total area.
If we wish to express the Ixy for the triangle in terms of its area, we call this quantity At; we can substitute At = 0.50*b*h, or half the base times the height. The final value of the product of inertia Ixy at the edge point- a, where the x-axis and y-axis intersect.
Rewrite the Ixy as AT*(1/12)*(2a+b)*h. The area At is the triangle’s total area.
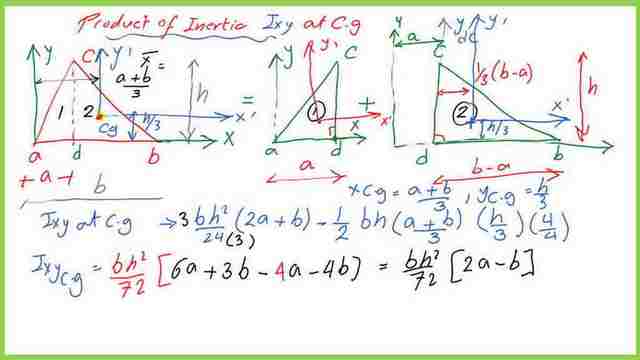
The value of Ixy for the triangle at the Cg.
The Cg of the triangle is located at x distance=1/3*(a+b), while y distance=h/3. These values are from Cg to the vertical axis Y at a and from the x-axis at the base of the triangle.
The final value of Ixy at the Cg is to be obtained by using the parallel axes theorem, and subtracting the product of the triangle area*xcg*ycg.
The final value of Ixy at the CG after subtracting (A*x-bar*y-bar). This is the final value of the product of inertia at the Cg, which equals b*h^2(2a-b)/72 as indicated in the following slide image.
This is the list of inertia for triangular shapes quoted from the NCEES tables of inertia. The estimated values for the product of inertia Ixy match the table,
You can download and review the content of this post through the following pdf file.
For an external resource, the definition of the moment of inertia with solved problems, 2nd moment of inertia.
For the next post, 16-Polar Moment of inertia– for the triangle.