Last Updated on March 11, 2024 by Maged kamel
Product of inertia Ixy for Right-angle triangle-case-2.
Product of inertia Ixy for right-angle by using a vertical strip.
1-For Ixy estimation, a vertical strip will be used, the strip width is dx and its height is y.
2- since the strip height starts from the base and is interested with line AC, y value is the same as the line AC equation y=h*x/b, for the x value it will be=b*y/h.
3- the moment of inertia due to that strip dIxy=dA*x-bar*y-bar) , our x bar =x, while ybar=y/2. Since we are integrating in the x-direction, we will substitute for – y value as (y=h*x/b ).

we will integrate from x=e from x=0 to x=b, the final answer is Ixy=h^2*b^2/8.
Product of inertia Ixy for right-angle by using a horizontal strip as an alternative.
1-For Ixy estimation, a horizontal strip will be used, the strip width is (b-x) and its height is y.
2- Since the strip height starts from the base and intersects with line AC, the y value is the same as the line AC equation y=h*x/b, for x value it will be=b*y/h.
3- the product moment of inertia due to that strip dIxy=dA*xbar*ybar) , our x bar =((x+0.50*(b-x))=1/2(b+x), while ybar=y. Since we are integrating in the y direction, we will substitute for x value as (x=b*y/h ). We will integrate from x=e from x=0 to x=b, the final answer is Ixy=h^2*b^2/8, which is the same value obtained by using a horizontal strip.

The same expression in the next slide is the integration of the dIxy from 0 to h of ∫(b^2)*(y*dy)- (1/2*b^2∫ y^3*dy/h^2). The integration of dIxy will be =Ixy and the b^2/2 will be the common factor.
For the first term y*dy the integration will be y^2/2 from 0 to h, (-) (b^2/2)*(y^4/4*h^2) when we are going to substitute when y=h.
We have (b^2/4)h^2- b^2/2((h^4/4h^2), it will become (b^2/8)( h^4/h^2)adjusting the terms, we have (b^2)(h^2)/4-(b^2h^2/8)=(h^2/8).

Product of inertia Ixyg for right-angle at the CG.
The product of inertia at the Cg Ixyg which is the product of inertia at the CG can be estimated by subtracting the product of A*x-bar*y-bar from Ixy value. For the Ixycg by using the parallel axes theorem, we have to deduct the multiplication of the area by (x*y). So Ixy at the Cg=Ixy-(area of the triangle *x bar*y bar)..
Our area for the triangle=( 1/2 *b*h), x-bar= 2/3 b, y bar =h/3.
So A (x-bar)*(y-bar) = (1/2)*( b*h)*(2/3*b)(h/3). 2 will go with 2 cancels each other, then we left we (b^2*h^2/9) so our Ixy at the CG=(b^*h^2/8)- (b^2*h^2/9), making the denominator as 72, we have (9-8) /72*(b^2*h^2). In the end, we will have (+1/72)(h^2)(b^2), which will be the value of the product of inertia at the C.G. for the right angle triangle.

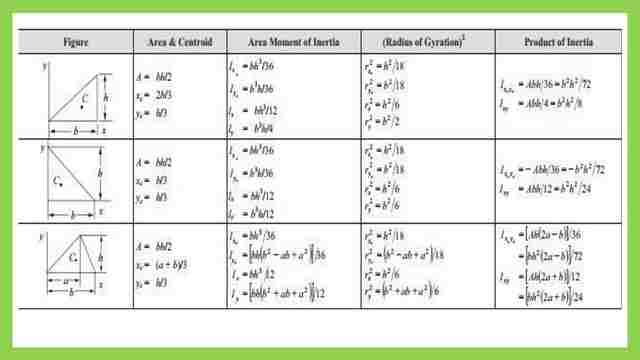
This is the table for the plain shape areas and their values of inertia.
This is the pdf file used in the illustration of this post.
For an external resource, the definition of the moment of inertia with solved problems, the 2nd moment of inertia.
This is the next post, Moment of inertia Ix for the triangle.
This is a link to my Playlist Moment of Inertia- English on YouTube.

