Last Updated on August 11, 2024 by Maged kamel

A Solved Problem 4-6-How to Find The Available Flexure  Strength?

A solved problem 4-6 for lateral-torsional buckling when lb>Lp but<Lr.

From Prof. Alan Williams’s book Structure -Reference manual,  solved problem 4.6 A W16x40 beam of grade 50 steel is laterally braced at 6 ft intervals. It is subjected to a uniform bending moment with the coefficient of moment Cb =1.0.

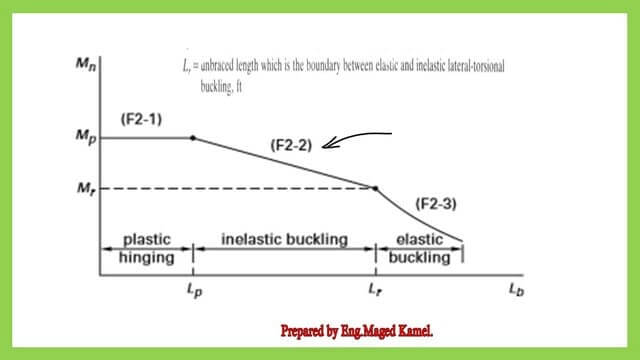
Determine the beam’s available flexure strength. This graph represents the relation between Lb and the nominal moment Mn; it has three zones based on the value of bracing length Lb and its relation with Lp and Lr.   

Analysis for the given section by the LRFD design.

The solved problem 4-6 is an analysis problem, the section is given for which, the distance between bracing for a beam is Lb > Lp, but Lb <Lr, for the LRFD design. it will fall in the second zone of inelastic buckling; please refer to the next slide for more details.

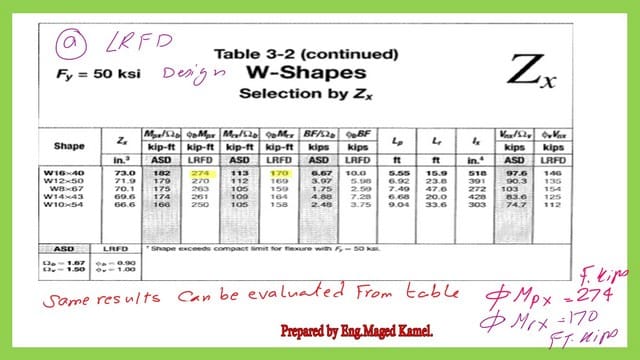
We need to find both bracing lengths lp and Lr for the given W section, which can be obtained from Tables 1-1 and Table 3-2. From Table 1-1, we need the value of ry to estimate the Lp value. For lr we need plenty of data to find lr as we will see next.

Get the maximum un-braced length to let the shape reach its plastic moment strength Lp. The relevant equation for Lp is introduced from Lp=300*ry/sqrt(Fy). We need to get these data from AISC table 1-1. The LP value is 5.55 feet. Our given bracing length is 6 feet, and the condition is that the bracing length is bigger than Lp. Please refer to the slide image for more details.

We need the following values from the Torsional properties: J, CW, and other properties, tf, Sx, rts, ho, selected from Table 1-1.

This is the equation for the L_r formula using equation F2-6.

This is the detailed reference equation number as presented in the AISC code.

This is the detailed estimation of the value of Lr using the equation.Lr=15.9′.

This is the value of limiting laterally unbraced length Lr using Table 3-2 for W16x48.

For the given Lb check if  Lb>Lp and Lb  <Lr, then the section is not compact, the value of φb*Mn is < φb*(Mpx), but φb*Mn > φb*(Mrx),  where Mpx=Fy*Zx,  while  Mrx= (0.70*Fy*Sx).

Estimate φb*Zx*Fy for Lb and φb*Fy*Sx for  Lr. Estimate the value of φb *BF.

The next picture explains the final φb*Mn= φb (Zx*Fy)—φb *BF*(Lr-Lb).
The available flexure strength is based on the LRFD, φb *Mn=269.50 Ft.kips.  

This is the value of φb*Mp and φb*Mr by using Table 3-2.

I have used an Excel plot to show the relation between Lb and φb*Mn.

The analysis for the given section by ASD.

We will use Table 3-2 to get (1/Ωb)*Mp and (1/Ωb)*Mr. We also get Lp and Lr values for W16x40.
  The given bracing length lb of 6 feet is bigger than Lp but smaller than Lr.

The section is not compact, the value of Mn/Ω is < (Mpx)/ Ωb, > (1/Ωb)*(Mrx)
Mpx=Fy*Zx, Mrx= (0.70*Fy*Sx).

Estimate (1/Ωb)*Zx*Fy for Lb and (1/Ωb)* 0.70*Fy*Sx for Lr.   
The final (1/Ωb)*Mn= (1/Ωb) (Zx*Fy)- (1/Ωb) *Bf *(Lr-Lb).
The available flexure strength based on the ASD, (1/Ωb)*Mn=179.00 Ft.kips.

These are the detailed calculations for the ASD moment value using BF, as shown in the next slide image.

I have used an Excel plot to show the relation between Lb and (1/Ωb)*Mn.

Please follow the Lateral Torsional Buckling Limit State for a valuable external source.
This is the solved problem 4-5.
For the next post, A Solved problem 9-7, When Lb>Lr, what is flexure strength?