Last Updated on April 28, 2024 by Maged kamel
Solved problem 4-6-block shear for a C-Channel-2/2.
This is the second part of the solved problems 4-6. We continue to find the block shear allowable strength for the channel and check the adequacy of the C channel against the total load.
We will check the block shear strength for the gusset plate based on the LRFd design and the block shear allowable strength based on The ASD design.
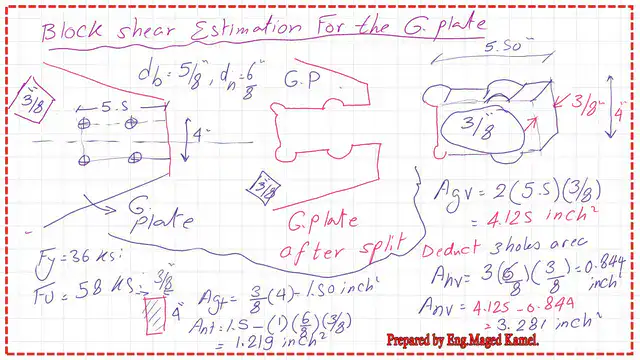
Estimation of Agv, Anv, and Ant for the Gusset plate.
We have a Block shear of size 5.50″x4″. The Gusset plate thickness is 3/8 inches. The gross area for shear will be equal to 2*5.50*3/8=4.125 inch^2.
To get the net area for shear, Anv deducts 3 hole areas; the bolt diameter is 6/8 inches. The final value of Anv equals 3.281 inch2. to get the gross area, we have a height of 4 inches and a Gusset plate thickness of 3/8 inches; the Ant equals 4×3/8=1.50 inch^2.
For the net area for tension, Ant deducts 1 hole area, Anv =1.219 inch2. Please refer to the next slide to check the full data for these calculations.
Estimation of LRFD design block shear strength for Gusset plate.
Let us review the gusset plate data for the gross and net areas. We have the values of Agv=4.125 inch2, Anv=3.276 inch2, Agt=1.5 inch2, Ant=1.219 inch2, and Ubs=1. The Yield stress Fy=36 kSI and Fu =58 ksi.
For LRFD design, φ equals 0.75. To calculate shear yielding and tensile rupture, multiply φ*(Agv*0.60*Fy+UBs*Ant*Fu), which is 0.75*(4.125*0.6*36+1*1.219*58)=119.85 kips.
For LRFD design, φ equals 0.75. To calculate shear and tensile rupture, multiply φ*(Anv*0.60*Fu+UBs*Ant*Fu), which is 0.75*(3.726*0.6*58+1*1.219*58)=182.688 kips.
We will select the minimum value equal to 119.85 kips. The plate is adequate for block shear since the ultimate load of 75 kips is less than 119.85 kips.
Estimation of ASD allowable block shear strength for Gusset plate.
For ASD design, Ω equals 2.0. To calculate shear yielding and tensile rupture, multiply 1/Ω*(Agv*0.60*Fy+UBs*Ant*Fu), which is 1/2*(4.125*0.6*36+1*1.219*58)=79.90 kips.
For ASD design, Ω equals 2.0. To calculate shear and tensile rupture, multiply 1/Ω*(Anv*0.60*Fu+UBs*Ant*Fu), 1/2*(3.726*0.6*58+1*1.219*58)=91.344 kips.
We will select the minimum value of 79.90 kips. Since the allowable load of 54 kips is less than 91.344 kips, the plate is adequate for the allowable block shear strength.
Estimation of ASD allowable block shear strength for C channel.
For ASD design, Ω equals 2.0. To calculate shear yielding and tensile rupture, multiply 1/Ω*(Agv*0.60*Fy+UBs*Ant*Fu), which is 1/2*(2.42*0.6*36+1*0.715*58)=46.871 kips.
For ASD design, Ω equals 2.0. To calculate shear and tensile rupture, multiply 1/Ω*(Anv*0.60*Fu+UBs*Ant*Fu), which is 1/2*(1.925*0.6*58+1*0.715*58)=54.23 kips.
We will select the minimum value of 46.871 kips. Since the allowable load of 54 kips is bigger than 46.871 kips, the plate is inadequate for the allowable block shear strength.
There is a very useful external link-Block Shear Rupture.
For the next post, Block shear and coped beams,