Last Updated on November 10, 2025 by Maged kamel
Practice problem for the x and y coordinates of a trapezoid.
In this post, we will introduce a practice problem for a Trapezoid’s x and y coordinates.
As we can see in the next slide image, a given trapezoidal area is drawn with the left side coinciding with the y-axis, with length a, and the lower side coinciding with the x-axis , with length h. The right side of the trapezoidal area has length a.
How to find the X-bar for the trapezoidal area?
The area can be considered composed of two triangles, and there is another position, which is to consider it a rectangle with a triangle. For the x Coordinate, I will use two triangles. The first triangle has base a and height h; the base coincides with the y-axis.
The second triangle has a base h and the height is b; the base coincides with the X-axis.
As we know, the x-bar for the first triangle equals h/3, while the x-bar for the second triangle equals 2/3 h. The areas of the two triangles are estimated based on the base and height of each one.

The next step is to estimate the product of the area by the x-bar of each triangle to get the final value of the first moment of area for the Trapezoidal area.
The final value of the first moment of the area can be found to be equal to (h^2/6)*(a+2b).

When we divide the estimated first moment of the trapezoid’s area by its area, we can find that the required x-bar of the trapezoidal area is equal to (h/3)*(a+2b)/(a+b). Thus, we have completed part 1 of the Practice problem for the x and y coordinates of a trapezoid.

How to find the y-bar for the trapezoidal area? First option.
We will use two options to estimate the y-bar of the trapezoidal area. The first option is to consider the trapezoidal area as composed of the two triangles, as we did while estimating the x-bar.
From the first option, the area of the first triangle is (1/2)*b*h, while for its y cg, we further divide it into two parts; the first part is with base b and with y bar equals 2/3b, while the second part is with a base of (a-b) and its y cg is (b+1/3(a-b), which can be adjusted to (2b+a)/3.
We will proceed to finalize the y-bar of the first triangle. For more details, please refer to the next slide image.
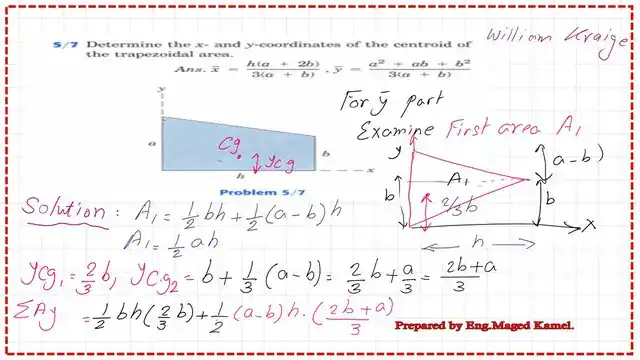
We will multiply each part by its y cg value for the first triangle to finalize the first moment of area for the first triangle. After adjusting the terms, we can find that the value is equal to h/6*(a^2+ab). Please refer to the next slide image for more details.

For the second triangle area A2, the area is equal to (1/2*b*h), and its y cg is (b/ cg is (b/3). The next step is to sum the first moment of the area of the first triangle with the first moment of the area of the second triangle, then divide by the area of the trapezoid. The final value of the Y-bar is equal to (a^2+ab+b^2)/(3)*(a+b). Thus, we have completed part 2 of the Practice problem for a trapezoid’s x and y coordinates.

How to find the y-bar for the trapezoidal area? Second option.
The second option is to consider the trapezoid as composed of a rectangle and a triangle. We estimate the area and the y cg of each area about the x-axis. Then, we sum the first moment of the area of the triangle and the rectangle. The next slide image provides a step-by-step guide.

We divide the area’s first moment by the Trapezoid’s total area. Y bar can be found to match the value estimated by Option-1. Thanks a lot.

For the estimation of the area and the Cg of a trapezium, please refer to post 8.
Efunda gives a helpful link for areas, and Cg can be viewed.