Last Updated on March 6, 2026 by Maged kamel
In Practice problem 5-8, the next step in determining the centroid for the shaded area involves a thorough analysis of the geometric properties within the specified region. By applying principles of calculus and geometry to the given shape, the precise coordinates of the centroid can be calculated with accuracy. This process will yield valuable insights into the structural integrity and balance of the area under consideration.
Practice problem 5-8. Find the centroid for the shaded area.
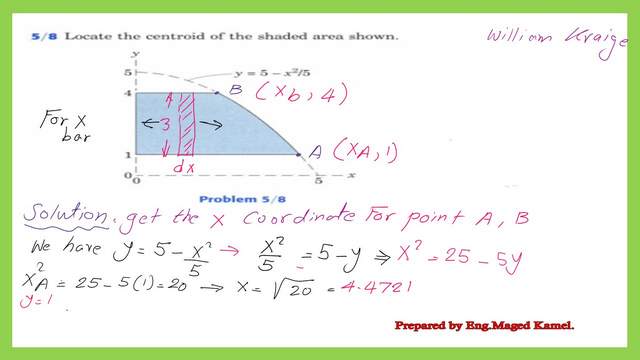
In this post, I will introduce practice problem 5-8. Find the centroid for the shaded area. The practice problem is quoted from Prof.William Kraige‘s book. The bottom side of the shaded area is 1 unit from the X-axis and coincides with the Y-axis on the left.
The shaded area is a composite section consisting of a rectangular portion with a height of 3 units and a curved portion with the equation y=5-(x2/5).
To locate the coordinates of the points on the curve, points A and B, we have the y-values of these points. We will substitute the value of y to get the corresponding X value.
Xa will be found to be equal to the sqrt(20)=4.4721. Please refer to the next slide image for more details.
Xb will be found to be equal to the sqrt(5)=2.23691.
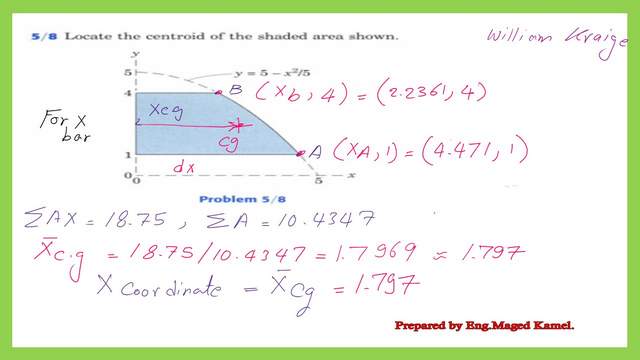
Find the first moment of area about the y-axis for the shaded area.
For the first moment of area about the y-axis, it is estimated as the sum of the integration of the rectangular strip of width (dx) and height equals 3 from zero to xb multiplied by x, and the integration of a strip of width (dx) and height (y-1) from xb to xa multiplied by x.
The height of the second strip is (y-1) since the base of the shaded area is shifted one unit up from the X-axis. To estimate the area of the shaded shape, we integrate a strip of width (dx) and height (y-1) from 0 to xb, then add the result to the integration of a strip of width (dx) and height (y-1). Please refer to the next slide image for more details.
We will perform the integration for the first moment of Area about the Y-axis and substitute with the values of Xa and Xb. The final value of the first moment of area about the Y-axis will be equal to 18.75.
Find the area of the shaded area.
We will estimate the area of the shaded region for the two parts. Again, we will substitute the values of XA and Xb. For the details of these calculations, please refer to the next slide image. The area is equal to 10.4347.
Find the X-bar for the shaded area and the x-coordinate.
It is easy to find the x bar, the distance from the Cg of the shaded area to the Y-axis, by dividing the value of the first moment of area about the Y-axis by the area. The final value of the x bar is equal to 1.797, which is the value of the x coordinate of the Cg point.
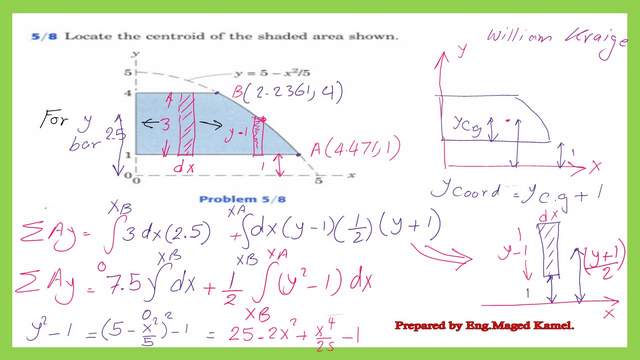
Find the first moment of area about the X-axis for the shaded area.
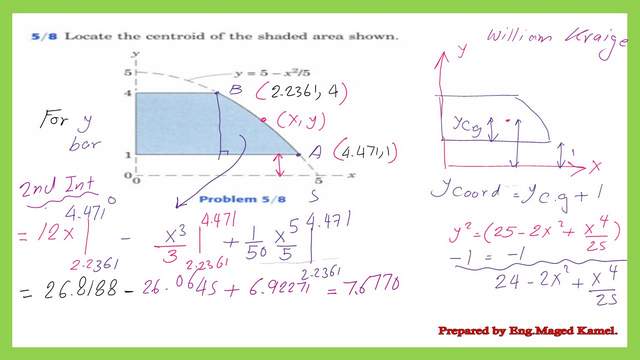
d the integration of a strip of width (dx) and height (y-1) from xb to xa multiplied by (1+y)/2. A detailed estimate sketch shows how to derive the y-bar for the second strip from the X-axis. The details of the estimate of the first moment of area about the x-axis are provided on the next three slides.
I have considered the second integration to simplify the calculation.
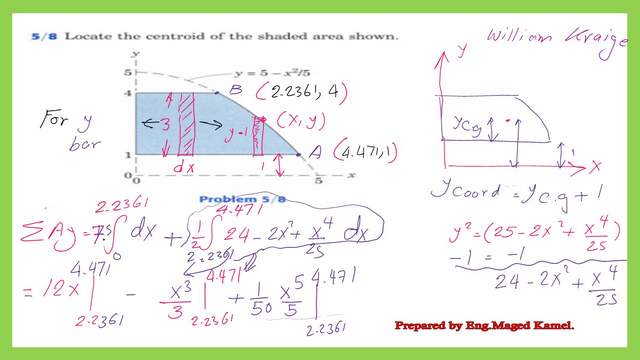
This is the value of the second integration for the first moment of area about the X-axis, which is equal to 7.6770.
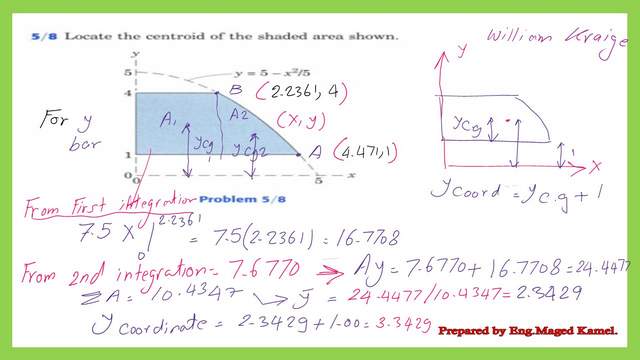
Find the Y-bar for the shaded area and the Y-coordinate.
We add the value of the first moment of area about the X-axis for the first integration for the rectangular portion to the second integration, and the final first moment of area about the X-axis is 24.4472.
It is easy to find the Y-bar, which is the distance from the Cg of the shaded area to the X-axis, by dividing the value of the first moment of area about the X-axis by the area. The final value of the Y-bar is equal to 2.3429. For the y coordinate of the CG, add one unit, so the value of the y coordinate will be equal to 3.3429. Thus I have completed the second requirement for Practice problem 5-8. Find the centroid for the shaded area.
The PDF of this post’s content can be viewed or downloaded from the following document.
This is a link to a beneficial, open, interactive site: Engineering Statics.
This is a link to the previous post. How to find the area and the centroid of a circular segment?