Last Updated on February 14, 2026 by Maged kamel
Introduction To Block Shear Resistance.
This is the content of the post.

Slenderness ratio as recommended by AISC.
The first part includes the code-recommended slenderness ratio L/r, which is preferred to be 300 to mitigate vibration effects.
Handling very slender sections is problematic; the main requirement is to hold without inadvertent bending.
Lifting a slender section by crane may buckle or be distorted during transportation and erection. Experience has shown that if you limit the slenderness L/r to 300,
You are less likely to have problems handling the member with the experience if we use a slenderness ratio L/r of 300.
The problems that occur during handling can be minimised: there is no strength limit state; the limit state is the same for both LRFD and ASD; and L/r is not related to LRFD or ASD parameters.

The code recommendation is in Chapter D, Design of Members for Tension, Specification 16.1, on page 28 of AISC 360-2016.
In Chapter D1, the slenderness ratio L/r for members designed based on tension should preferably not exceed 300. This suggestion does not apply to rods or hangers in tension.

The code recommendation is in Chapter D of the latest specification, Design of Members for Tension, Specification 16.1, on page 32 of AISC 360-2022.

How do we derive the equation for block shear for tension members?
If bolts join two pieces, they are subjected to two equal and opposing tensile forces.
After studying one section, we will discover that the tensile force may be divided into two components: one is perpendicular to part bc, as shown in the illustration.
In contrast, the other component generates shear in part ab. There will be two types of fractures: yielding and rupture for tension and shear stresses.
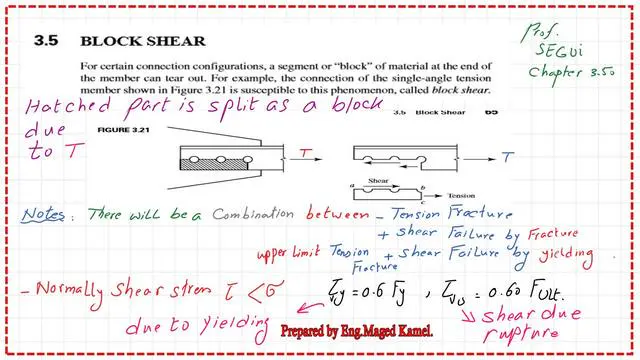
The failure does not extend to the upper part of the angle since it is considered a stiffened end.
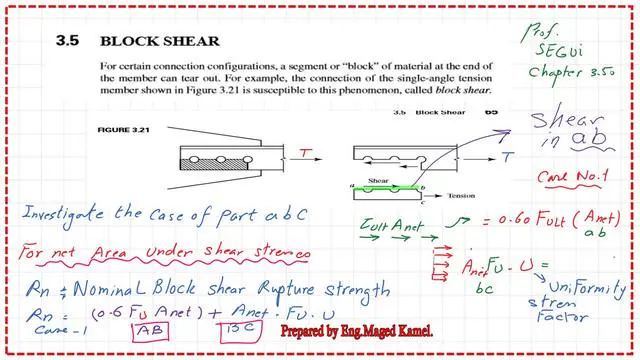
Block shear Formula.
This is the nominal value Rn, calculated using a two-part formula: one for shear and one for tension.
The expression for Area Agv is the gross area with a shear component, and we do not deduct the bolt area. While Ant is the net area with a tensile component, from which we deduct the bolt area. The shear stress is taken as 0.60 times the tensile stress.
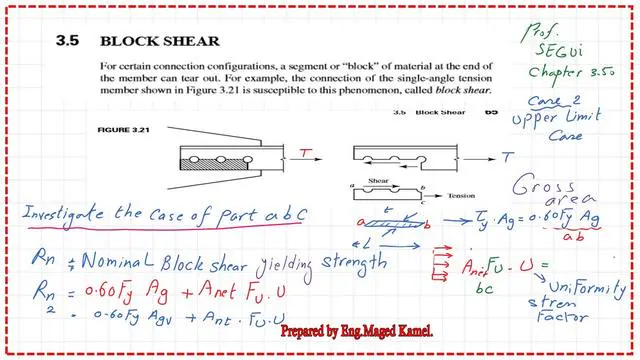
The difference between the upper limit and the lower limit.
The difference between the upper limit of fracture and the other limit of failure will be considered as follows: The upper limit of fracture combines Tension failure by rupture and shear failure by yielding.
The shear fracture term is the product of Anv x0.60Fu, while the shear yielding term is the product of Agv x0.60FU.
The tension rupture term is the product of Ant, Ubs, and Fult. This term is common to both the lower and the upper bound.
For the LRFD design, we multiply the maximum value of the two cases by phi, which equals 0.75. For the ASD design, we multiply the maximum value of the two cases by (1/omega), and Omega equals 2.

UBS values vary with the uniformity of stress distribution across angles and guest plates. Most coped beams have a uniform stress distribution. The second case is where Ubs = 0.50 for a nonuniform stress distribution. The UBS values are shown in the next slide image.

The next slide is the reference in the specs for Chapter J, which concerns connections. The specification provides for steel connections.

In the next slide, the equation for the block shear strength is J4.5.

This si the provision of J4.5 in the specification of 2022.

The PDF file for this post can be viewed or downloaded from the following link.
The following post is a Solved problem 4-4, How to get Pult without block shear.
There is a very useful external link, Block Shear Rupture–A Beginner’s Guide to the Steel Construction Manual, 14th ed.
There is a very useful external link, Block Shear Rupture–A Beginner’s Guide to the Steel Construction Manual, 15th ed.
There is a very useful external link, Block Shear Rupture–A Beginner’s Guide to the Steel Construction Manual, 16th ed.