A Solved problem 4-4, P Ult Without Block Shear.
At the beginning of this post, we will review the equations for tensile yielding and Tensile ruptures and the different Phi values for the LRFD design case.
A Solved problem 4-4.
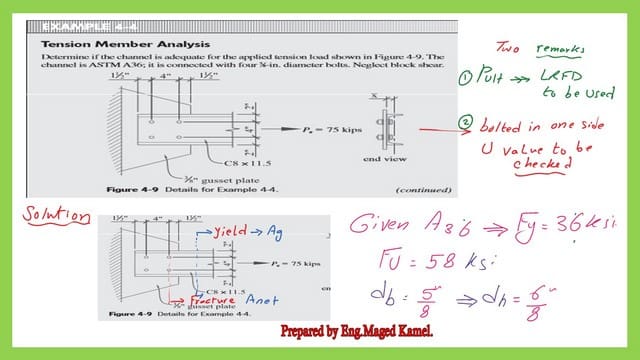
In the solved example 4-4 from Prof. Abi O. Aghayere’s handbook, it is required to estimate the ultimate tensile force of a channel C8x11.50 connected to a gusset plate by two lines of bolts.
Each line has two bolts. To check the section’s adequacy, neglect the Block shear and compare the ultimate load value of 75 kips to the estimated design nominal load by the LRFd design.
The bolts are 5/8 inch each. Given Fy=36 ksi, while Fult=58 ksi.
For the state of rupture, we need to estimate the effective area for a section perpendicular to the force direction. The deduction of bolts takes into consideration adding 1/8″, and the diameter of the hole is 6/8 inches.
Limit state of yielding.
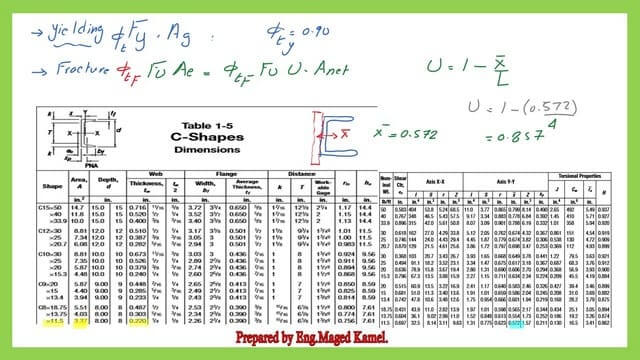
For the state of yielding, we need to estimate Fy*Ag, Fy=36ksi, Ag=area of a channel without deduction, from table C 8×11.50=3.37 inch2, tweb=0.22 inch. The necessary data are obtained from Table- 1-5 for the C channel.
Limit state of rupture for the solved problem 4-4.
We use Table 1-5 for C shapes and select channel C8x11.50.The value of the gross area is equal to 3.37inch^2.
It is required to estimate the U factor from the relation U=(1- x̅ /L); we have a neutral axis distance about the y-axis, which is written as x- bar from table 1-5, which is assigned for C channel sections, is taken as x̅=0.572, the shear lag factor U=(1-0.572/4)=0.857.
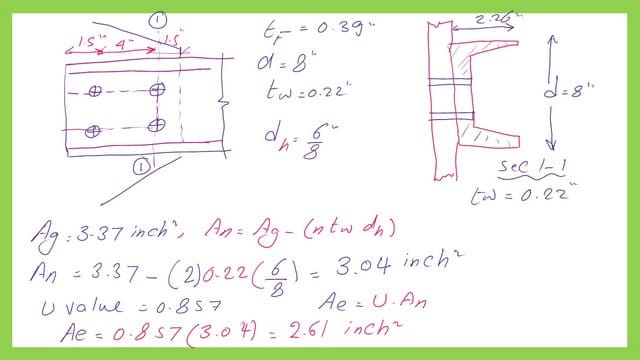
The next slide images show the sketch of the C channel and the spacing between bolts; for sections 1-1, we need to deduct the area of two holes, where the diameter of hole dh equals 6/8 inches, and web thickness is 0.22.”
We will estimate the net area by deducting the product of (2*6/8*0.22)=0.375 inch2.
The net area will be equal to 3.37-0.375=3.04 inch2. To get the effective area, multiply the net area by the U factor. The U factor is equal to 0.857. the final effective area is equal to 2.61 inch2.
If the block gear is neglected as required, we list all our data: the gross area, which is equal to 3.37 inch2; A36 steel, with the yield stress Fy equal to 36 ksi; and the ultimate stress Fu, which equals 58 ksi.
The nominal load based on yielding is equal to the product of gross area by the yield stress; in this case, the nominal load is 121.32 kips. To get the design nominal load due to yielding, multiply 121.32 by phi, which equals 0.90; the value will be 109.188 kips.
The nominal load based on rupture is equal to the product of the effective area by the ultimate stress; in this case, the nominal load is 151.38 kips. To get the design nominal load due to rupture, multiply 151.38 by phi, which equals 0.75; the value will be 151.535 kips. Select the lesser value, which will be equal to 109.188 kips.
Compare the given Pultimate value of 75 kips with the selected nominal design value of 109.20 kips. The section is adequate since Pult is less than the LRFD design value. The next slide image shows the full details of the previous calculations.
There is a very useful external link-Block Shear Rupture.
This is the next post, Solved problem 4-6-block shear for a C-Channel-1/2, in which we solve a problem and get the ultimate tensile force after considering the block shear.
