Last Updated on June 15, 2025 by Maged kamel
The similarity between cash flows and forces.
Introduction to Cash Flow and Equivalence.
There is a similarity between cash flows and forces. The economic equivalence can be viewed as a relation between two forces acting on the free body diagram, the sum of the moments due to those two forces can be set equal to zero.
As colleagues as mechanical and civil engineers, we are familiar with both bending moment and shear forces and how to get the bending moment for a given beam.
The moment due to cash flows is nothing but the multiplication of cash flow by the distance to the point located in the timeline. Whether the cash flow is inflow or outflow, when drawn as a timeline; the horizontal line starts from time t=0 and ends at time t=n.
The cash flow can be represented as an upward arrow when you have an income, from the borrower’s point of view. While expenses are drawn as a downward arrow, for the present value P. For instance, it is required to find the future value F. The picture is quoted from the book Engineering Economic Analysis, 11th edition. The author is Donald G Newman. The chapter titled ECONOMIC EQUIVALENCE VIEWED AS A MOMENT DIAGRAM.
Another payment, shown as F, is needed to pay the loan back; the directions of both P and F will be opposite each other.
The present value, while paying, is represented by a downward arrow, or (-) P. When we have an income at present. P is represented by an upward arrow or (+P). And similarly, for future values, income is upward, while paying is a downward arrow.
If you consider the cash flow as a group of forces that are always perpendicular to the axis, then the periods become the distance along the axis.
We need the distance between the forces along the Timeline. We know that there is an equilibrium at any point in the moment diagram; this is applied at the point from all directions.
As we know, in the bending moment diagram for a beam, at a certain point, we will have both clockwise and anti-clockwise moments.
The summation principle will lead to a zero value of the moment. I quote that we are assuming that clockwise rotations are positive. This principle allows us to assume that the positive forces point up and that positive distances are measured from left to right. How does this technique work?
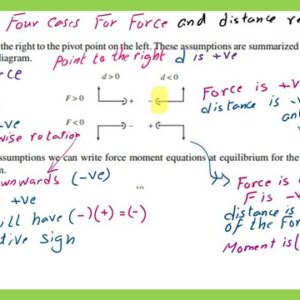
The different cases of forces, cash flows, and the pivot point.
We will discuss the different cases Of forces and the moments produced by these forces, whether positive or negative.
If they are bigger than 0 and pointing up, they can be represented by the (+) sign. A moment due to a positive force at a point on the right side of that force is a clockwise moment that is positive.
We have four cases. The first case is the case of an upward force, and the point is on the right side. In the second case, the force is acting upwards, but the moment is about a point at the left side of the force, then the moment as a product of (+)*(-) =(-) is considered negative as being anticlockwise rotation.
The third case, where the force is pointing down, is considered as (-) value, and the point we are getting the moment at lies at the right side, the moment as a product of (-)*(+) =(-) is negative as being anticlockwise.
In the fourth case, where the force is pointing down, considered as (-) value and the point we are getting the moment at lies at the left side, the moment as a product of (-)*(-) =(+) is positive as being clockwise.
The written data concludes the previous four cases we have just explained. The slide image shows the four cases for forces and the distance to pivot points.
Cash flows moments and moments due to forces.
A s a similarity between Cash flow moments and moments due to forces. We consider the following points:1- A sign convention for cash flows, such that positive values point up. For instance, that represents inflows, the bank point of view is (+), while the moment arm is at a pivot point.
To measure the moment arm as (1+i)^T, where i is the interest rate, whether yearly or monthly, based on the given case.
While T is the number of periods, that is the distance measured from the cash flow to the pivot point or axis of rotation at the stated point.
Thus the sign of the distance is moved to the exponent, with its sign whether (+) or (-).
For cash flow at the pivot point, T=0 and (1+i)^0=1, and in that case, the moment value will be the exact value of the force value. For a given example, P acts at a pivot point with unknown present cash flow where T=0.
P is considered downward(-P). Money was paid, and it is expected to receive +10 in the third year and at the end.
For instance, you will pay (6) at time t=5, which is represented by the downward -6. We have +10 acting upward &while P as the present value is -P and -6. Let us consider the bending moment at a pivot point at t=1.
The sum of the moments at the pivot point (t=1) will be equal to 0. Start with (-P), which creates a moment at t=0. The point is at the right, with T=1.
The moment arm will be (1+i)^1. Now consider the (+10) that acts on t=3, since the pivot point is at the left side of the (+10), then the difference between T=3 and T=1.
The moment due to +10 will be=(1+i)^(-)(3-1) or (1+i)^(-2). To consider the moment due to T=6, the force is acting downward; then, it will be=-6. The arm of the moment is (1+i)^-(5-1)=(1+i)^-4. The sum of the moments is zero.
Now let us review the written expression,-P*(1+i)^1+10*(1+i)^(-2)+(-6)*(1+i)^-4=0. When rearranging the terms, we can get an expression for the P value. The slide image describes the moment arm and the acting forces.
Please click on any image, and you will have a slide show. Each photo will appear more transparent.


Please refer to this post, Introduction to Economic Equivalence, to review the subject of equivalence.
The next post: Derive the P and F relation as cash flow moment.
This is a good link -Engineering Economy. A good referance
