Last Updated on March 21, 2024 by Maged kamel

What is Economic equivalence?

Solved problem 1-2, how to get the past value of an invested money for a given interest rate, given time?

The example is from Leland Blank, Anthony Tarquin’s handbook, basics of Engineering Economy.

Example 1.2 a) Calculate the amount deposited 1 year ago to have $1000 now at an interest rate of 5% per year.
B) calculate the amount of interest earned during this time period. We have an investor who deposited one year ago, at an interest rate of 5%, and he received $1000 now, this is the case of an investment, someone has deposited an amount of money at a rate of 5%.

The original amount of money is unknown, provided that the investor has received $1000 now, the formula states that the interest =money amount obtained now- original deposit. The interest rate that is given as 5%, can be written as I%=(Money amount now – original deposit)/ original deposit,

The original deposit can be rewritten as= Money received now/(1+I%). Original*(1+0.05)= money received now.

The required amount of the original deposit=1000/1.05=$952.38. This is part a- of the solved problem, please refer to the next slide image.

This part b where the amount of interest can be estimated as interest value=Final amount- initial amount=1000-952.38=$47.62. This is the formula from which the interest rate was estimated.

The second solved problem 1.4

Another example 1.4, A Stereophonic Incorporation Plans to borrow $20000 from a bank for one year 9% interest, for new recording equipment.
a- it is required to estimate the interest and the total amount due after one year.
b-construct a column graph starting with $20000 as the original amount borrowed.
The solution: The given interest rate is 9%, and the Incorporation should repay $20000 + 9% per/1 year*original amount. The Interest amount=0.09*20000=$1800, to be added to the original amount. The total due is =20000+1800=$21800.

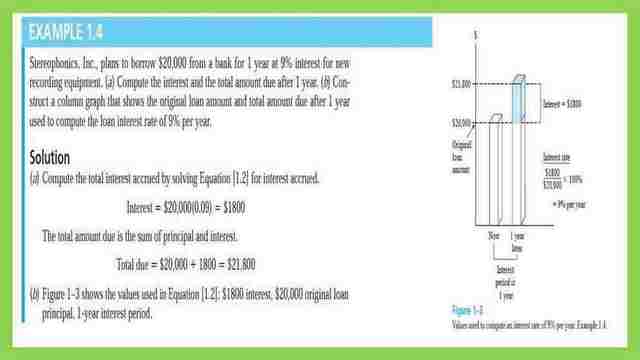
In the graph he makes a comparison between the two graphs, which is drawn based on two axes, the horizontal axis X represents the time elapsed and the vertical axis y represents the amounts in dollars, the first graph has a height of $20000, while the second graph with a height=2000+1800=$21800.

Economic equivalence.

There is another subject which is engineering equivalence, the equivalent in other subjects is used to transfer between units and measures, for instance, 1 km=1000m, and one pound=0.4536 Kg. As for economic equivalence, it indicates a different amount of money at a different period.

The money value is considered equal to the time value for it. Considering the time value of money the following simple example will explain the meaning of the equivalence. The value of money -now= the future value of money after considering a specific rate and again is = past value of money after deducting the interest rate.

Let us have a look at an example, what is the equivalent amount of $100, after one year, and one year before? Future value of money =money value now*(1+interest rate%)=100*(1+0.06)=$106.

The money amount from one year before is related to the money now, from the formula, money one year before*(1+interest rate%)=money now.

Money one-year before=money now/(1+interest rate%)=100/(1+0.06)=$ 94.34.
Both values whether$100 or $ 94.43 are equivalents provided that for these amounts same interest is used which is 6% in this example.

$100 of interest=6% one year from now will be equivalent to =100*(1+0.06)=$106.
While the same $100 of interest 6%, one year ago will be equivalent to =100/(1.06)=$94.34.

The next figures show the equivalence values of the three amounts of money with a given interest value, the -axis represents the time interval, and also a histogram for the time value of money. While, for the value of one year before 6%, it is = $94.36 and is shown in the first histogram. The second histogram is for the value of money now, which is= $100.

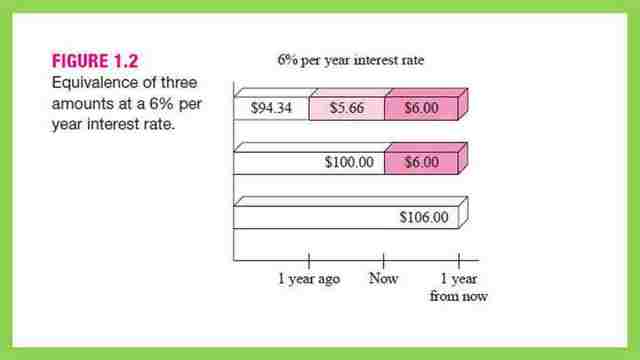
For one year from now, add $6.00, this is shown in the third histogram.
The economic equivalence assumes that $100 money now = $ 106 money after one year=$94.34 one year before.

This is the Pdf file used in the illustration of this post.

The next post is A Solved Problem for Economic Equivalence.

Engineering Economy Applying Theory to Practice is a good reference.