Last Updated on June 4, 2024 by Maged kamel

List of Steel beam posts-part-1.

Steel beams and types of buckling-List of Steel beam posts-part-1.

This is the first post of the Steel beams  Posts, which includes:
 1-Definition of steel beams. Sketch showing the different parts of a frame.
 2—Causes of failure for beams. The beams can fail while reaching the plastic moment or one of the three causes: LFB-local flange buckling, LWB Local web buckling, and LTB lateral-torsional buckling. Detailed descriptions of the three cases are given as sketches and a resource.

This is the link to the first post: Steel beams and types of buckling.

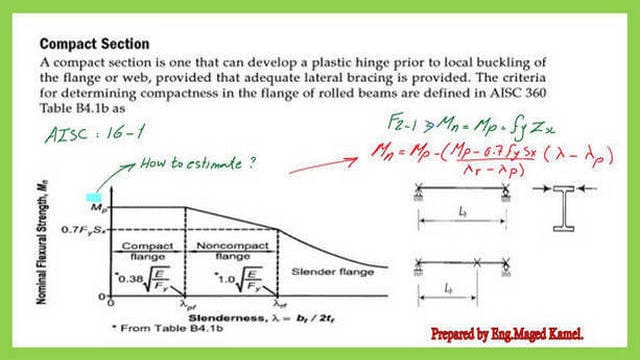
An easy approach to the Compact and non-compact sections.

    This is the second post of the Steel beams  Posts, which includes:
   1-Definition of compact section.
  2-The value of Mp-Fy*Zx.
   3- AISC Table B4.1 for the width-to-section ratio for compression elements,  members subject to bending.

The next slide is one of the slide images included in the post.

This link is for post 2: An Easy Approach to Compact and Non-compact section. 

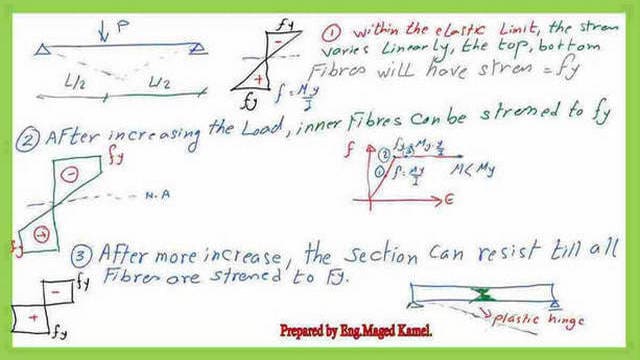
An Easy Introduction to Plastic Theory for Beams.

This is the third post of the Steel Beams Posts, which includes an introduction to plastic theory, the stress-strain curve for steel, a review of the allowable stress design ASDM, the definition of a plastic hinge, and an analysis of a rectangular section for any shape.

The next slide is one of the slide images included in the post.

This link is for post 3: An Easy Introduction to Plastic Theory for Beams. 

 An Easy Introduction to Plastic Theory for Beams.

The post includes three terms: modulus Sx and how to estimate it. When we have a rectangular section (b*h) under a moment, the stress at the upper fiber has reached yield. The section modulus Sx equals My/Fy, where I am the yielding moment, and Fy is the yield stress. It can be found to be equal to b*d2/6 for a rectangular section.

The plastic section modulus is termed Zx and equals Mp/Fy, where Mp is the plastic moment, and Fy is the yield stress. For a rectangle, Zx equals b*d2/4. The third item is the shape factor, which is Zx/Sx. More details on estimating Sx and zx values for any shape are given.

The next slide is one of the slide images included in the post.

This links to post 3a: An Easy Introduction to Plastic Theory for Beams. 

Solved problem 4-3  for the elastic and plastic section moduli.

This is the fifth post of the Steel Beams Posts, which includes a solved Example 4-3, quoted from the structural engineering reference manual.
 
Determine the plastic section modulus and the shape factor for the steel section shown. Assume that the section is compact and adequately braced. To get the shape factor, we must find the elastic section modulus Sx. Sx can be estimated as equal to Ix/Sx. There are two ways to get the value of Ix.  

Find the plastic axis that divides the T section into equal areas to get Zx. Zx = (At/2)* (y1+Y2). The shape factor equals Zx/Sx. The next slide is one of the slide images included in the post.

This link to post 4: solved problems 4-3 for the elastic and plastic section moduli. 

A Solved problem 5-1 for Sx & Zx-elastic-plastic moduli.

This is the sixth post on the list of steel beam posts, which includes a solved problem from Prof. William T. Segui‘s book.

 Example 5.1 For the built-up shape shown in Figure 5.6, determine (a) the elastic section modulus S and the yield moment My and (b) The plastic section modulus Z and the plastic moment Mp. Bending is about the x-axis, and the steel is A572 Grade 50.

This problem is similar to solved problem 4-3 included in the previous post. The only added step is multiplying Zx by Fy to get the plastic moment value.

The next slide is one of the slide images included in the post.

Part (b) Find the plastic section modulus Z and the plastic moment Mp. Bending is about the x-axis, and the steel is A572 Grade 50.

This is a link to post 5: A Solved problem 5-1 for Sx & Zx-elastic-plastic moduli. 

 A Solved problem 5-2 for Sx&Zx and shape factor. 

 This is the seventh post of the Steel Beams series, containing a solved problem from Prof. William T. Segui‘s book.

Example 5.2  Compute the plastic moment, Mp, for a W10 × 60 of A992 steel. Two methods are used for the solution. The first method considers the W section to be composed of several plates.

The second method uses Table 1-1 to get the relevant data. The post explains the complete details for finding Sx, Zx, and Plastic moments.

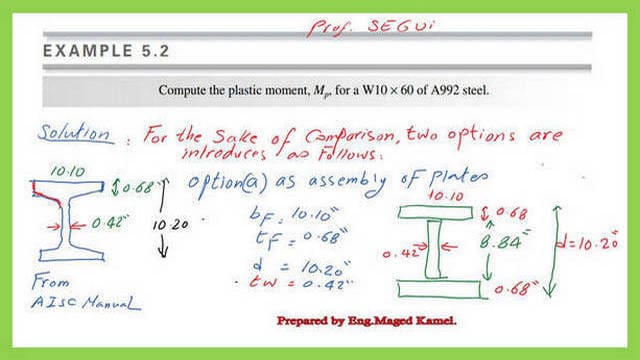
This link to post 6:A Solved problem 5-2 for Sx&Zx and shape factor.

Practice problem 5-2-2: Find y bar, Zx, and Zy for the un-symmetric section.

This is a newly added post. It is a step-by-step guide for solving practice problem 5-2-2, which includes an unsymmetric section for which the Y bar from the flange top to the Cg of the plastic neutral axis must be found. The plastic moment must also be found for a given steel grade, and finally, the plastic section modulus Zx must be found.

This is the link to post 6a.

Practice problem 5-2-3 verify Zx for a given W 18×50.

This is a newly added post. It is a step-by-step guide for solving practice problem 5-2-3, which includes a W18x50 steel section for which the plastic section modulus Zx must be verified. Two methods are used for verification.

This is a link to post 6b.

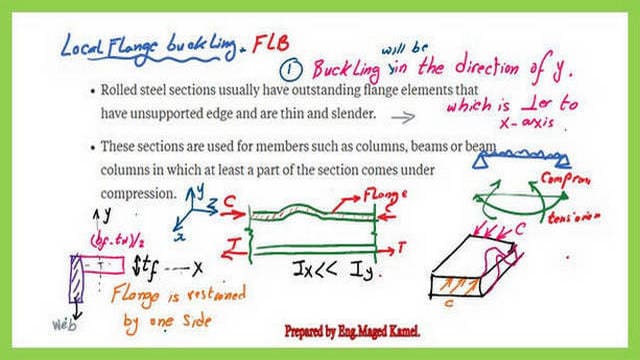
Local buckling parameters for steel beams.

This is the 8th post of the Steel beams Posts, which includes lambda λp and λr values for compact and non-compact flange and web for The W section. What are the stiffened and unstiffened elements? How do you get the Fcr value? A more detailed illustration of Local buckling parameters is given. A discussion of the AISC table B 4.1B is presented.

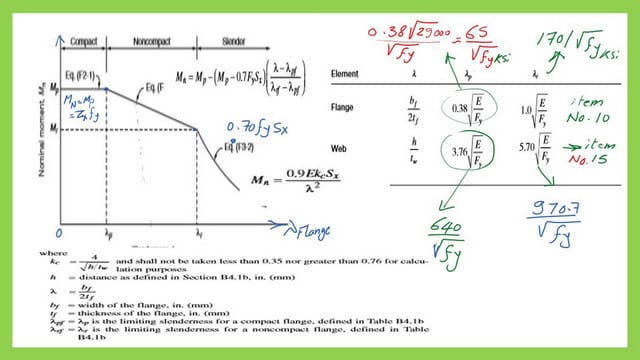
This links to post 7: Local buckling parameters for steel beams. 

How do we analyze steel beams? Solved problems.

This is the 9th post of the Steel Beams Posts, which includes a Solved problem from Prof. William T Segui‘s book, Example 5-3. The beam shown in Figure 5.11 is a W16 × 31 of A992 steel. It supports a reinforced concrete floor slab that provides continuous lateral support of the compression flange. The service dead load is 450 lb/ ft. 

This load is superimposed on the beam; it does not include the weight of the beam itself. The service live load is 550 lb/ ft. Does this beam have adequate moment strength?

 This load is superimposed on the beam; it does not include the weight of the beam itself. The service live load is 550 lb/ ft. Does this beam have adequate moment strength?

The second problem solved is in Eng Lindeburg ‘s book. Establish whether the W21x55 beam of A992 is compact with given four options to check the correct one.

This is a link to post 8: How to analyze steel beams? Solved problems.

 A Solved problem-7-4-1: how do we design a steel beam?

  This is the 10th post of the Steel Beams Posts, which includes a Solved problem from Prof. Charles G. Salmon’s book.

Solved problem 7-4-1  Select the lightest W or M section to carry a uniformly distributed dead load of 0.2 kip/ft superimposed (i.e., in addition to the beam weight) and 0.8 kips/ft live load.

The simply supported span (Fig. 7.4.2) is 20 ft. The compression flange of the beam is fully supported against lateral movement. Use Load and Resistance Factor Design, and select the following steels: A36, A992, and A572 Grade 65.

This is a link to post 9: Solved problem-7-4-1, how to design a steel beam.

A step-by-step guide to Lateral-torsional buckling

This is the 11th post of the Steel beams Posts. A new subject is the Lateral-torsional buckling of beams. A torsion will occur for a beam accompanied by a lateral movement, which refers to the definition from Schaum’s book, Structural Steel Design—introduction to the Coefficient of Bending CB. 

This is a link to post 10: Step-by-step guide to Lateral-torsional buckling.

This is the link for the second post, List of steel beam posts-part 2.

A very useful external resource is A Beginner’s Guide to Structural Engineering.