Elastic And Plastic Section Moduli.
First, we start with the elastic section modulus called Sx. When we have a rectangular section (b*h) under a moment, the stress at the upper fiber has reached the yield. The stress at the lower fiber has reached yield.
The beam will deflect like this shape due to the bending moment. The upper fiber will have compression stresses, while the lower fiber will have tension stresses.
If the load acting on a beam is increased, more than the load creates the first yield in the upper fiber until the stress Fy propagates from the upper fiber to a lower one and the section becomes fully yielded and thus, we get our plastic neutral axis.
The stress profile has changed from a triangle to a trapezium shape. Ultimately, it will become a rectangular shape, as shown in the sketch.
If we consider the symmetry, the area above the Plastic neutral axis is equal to half the area or A/2, where A is the total area of the whole section. A compression force will act on the upper section.
This force at plastic stage Cp=Fy* area of a rectangle (b*h/2), or Fy* area of a rectangle (b*h/2), there will be a tension force Tp equal to compression force Cp, for the lower portion below the P.N.A, Cp =Tp =Fy*(b*h/2).
Both forces will act on the Cgs, the center of gravities, at h/4 above and below the neutral axis. The term yct is the distance between the tension and compressive forces, be equal to (h/4)+(h/4)=h/2.
Let us write the following information in an equation, where Cp=Tp=Fy*A/2, while yct=h/2. The plastic moment Mp=Fy*(A/2)*(h/2).
A new term, Zx, or the plastic section modulus, will appear. The value of Zx=(A/2)*(h/2) =(b*h)/2*(h/2)=b*h^2/4 or Zx=(A/2)*2 y bar. This is one y bar distance, measured from the Cg of the upper area to the P.N.A. This why 2*y bar=2*(h/4)=h/2.
In the case of a rectangle, the plastic section modulus Zx=b*h/4. What is the shape factor, the shape factor? The shape factor is the ratio of Zx/Sx or (plastic section modulus/ elastic section modulus) it will be equal to 1.50.
Section modulus Sx for a rectangle shape-part 1.
This is a general way to estimate the section modulus for a rectangle at any axis, located at a distance Kd from the bottom of the rectangular section.
1-At first, it is required to get the Y bar for the section, by summing the first moment of areas, considering the datum line is at the bottom, the product of A1y1+A2*y2= At*y bar since the total area is known so that we can get- Ybar.
2- we estimate the inertia about the neutral axis, we have just evaluated at a distance y bar from the datum.
3- We estimate the y-max value, for a rectangle as y max=d/2, Sx is simply the division of Inertia Ix/ymax.

How to evaluate Zx, Plastic section modulus for a rectangle?
A- To estimate the Zx, the plastic section modulus assumes there is an axis that divides the whole section into two equal areas and assumes that it is apart by Kd distance from the datum line.
B-equate A1 and A2 and get the value of k, which is the case of a rectangle=1/2.
B-The product of (At/2 )*(y1+y2) will give us the plastic section modulus, where y1 is the distance from the P.N.A to CG of Area A1, while y2 is the distance from the P.N.A to CG of Area A2.
If we move to the next slide, due to the symmetry, the y bar which we have estimated is the distance from the bottom to the elastic neutral axis, will divide the rectangle into two equal parts.
The Sx value is to be equal to Ix /y max, where Ix equals bh^2/12, and the y max equals h/2.
The elastic section Modulus Sx for a rectangle will be equal to b*d^2/6. The elastic neutral axis will divide the shape into two equal parts due to symmetry for W, M, and S shapes.
For the c shape, it has a symmetric axis which is x-x, the NSA will pass by the X-axis.
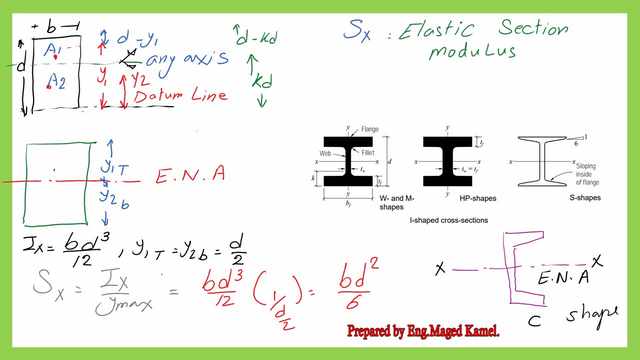

In the next slide, three shapes are doubly symmetric about both the X and Y axes, the EN axes pass by the X-axis.

A very useful external link to download PDF.Chapter 8 – Bending Members.
The second part of this post will include how to estimate the Elastic and Plastic Section Moduli for any section.
For a solved problem please refer to post 4-Solved problem 4-3 for the elastic and plastic section.

