Last Updated on June 9, 2024 by Maged kamel
How to design a steel beam? Solved problem-7-4-1.
This is the first part of the post on designing a steel beam using various steel types. In this first part, we will consider Fy=36 ksi and Fy=50 ksi. The second part of this post will consider A572 steel.
How to design a steel beam? Solved problem-7-4-1.
A steel beam with the lightest W or M section must be designed under a uniformly distributed load and a given live load. The beam’s compression flange is fully supported against lateral movement.
For Case#1- Design a steel beam with Fy=36 ksi.
For the first case of Fy=36 ksi, it is required to design a steel beam of W—section or M section for a simply supported beam of span =20′ for the three cases of Fy values.
Find the Ultimate Moment-Fy=36 ksi.
Starting with ASTM A36, where the Fy=36 ksi. The first step of designing a steel beam is to estimate the Ultimate load value of 1.20D+1.6L of the steel beam. Wult=1.2*0.20+1.60*0.80=1.52kips/Ft. The ultimate moment for a supported beam, Mult= wult*L^2/8. Mult=1.52*20^2/8=76 Ft.kips. This is the value of Multimate.

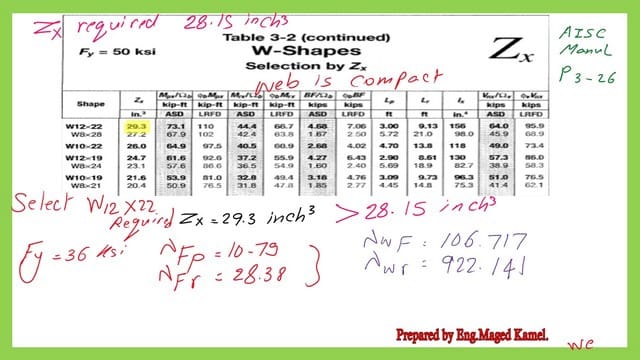
Determine the required Zx-select a section.
Our first trial is to equate Mult/(0.90*Fy)=Zx, get the Zx, and then check the table. The next slide shows the limiting slenderness parameters lambda λF and lambda λw for ASTM A36, where Fy=36 ksi, lambda λfp=0.38*sqrt*(E/Fy)=0.38*sqrt(29000/36) =10.79, while flange lambda λfr=1*sqrt*(E/Fy)=28.38. For web lambda λwp=3.76*sqrt(E/Fy)=106.72, whie for lambda λwr=5.70*sqrt*(E/Fy)=922.141.
The plastic section modulus equals 28.15 inch3.

We will use Table 3-2, where W sections are sorted by Zx; we find that W12x22 has a Zx value equal to 29.30 inch3, bigger than the required Zx.
Flange λ and web λ against local buckling parameters.
We will estimate the slenderness ratios for both the flange and web and the flange lambda λF, lambda λw and compare these values with the limiting values of lambda λp; based on the comparison, we will determine if lambda λF or lambda λw< lambda λp – plastic. From Table 1-1, in the second part, the flange λf=4.74 and web λ=41.80.
The next slide shows that section W12x22 is a compact section.
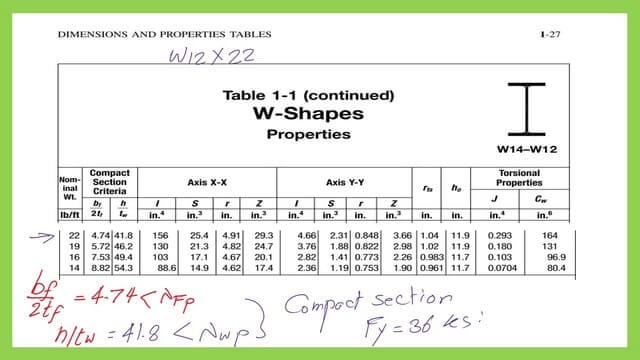
We will readjust the value of the ultimate moment by adding its weight—the new Mult=1.555*20^2/8=77.32 ft. kips.
Since our selected section is compact, Mn=Mp. Mp=Fy*Zx. For the LRFD, the value of Φb*Mn=Φb*Fy*Zx, which is Φb*Fy*Zx=79.11 Ft.kips.
Since the acting Multimate is only 77.32 ft. kips, the section is safe since 79.11 is >77.32 ft. kips.

For Case#2- design a steel beam with Fy=50 ksi.
Determine the required Zx-Fy=50ksi.
The second case for ASTM A 992, where Fy=50 ksi. Mult without the superimposed load was =76 ft. kips.
We need Zx to start with Table 3-2. Zx=Mult/(0.90*50)=20.22 inch3.
We will proceed to table 3-2, but select Zx>20.22 inch3, which will be W10x19 with Zx=21.60 inch3. Zx selected=21.60 inch3. We proceed to get the properties of our section. W10x19.

Local buckling parameters-Fy=50 ksi.
In the next slide, we find the local buckling parameters for Flane and Web based on Fy=50 ksi.

From Table 1-1 part 2, the λ for flange equals 5.09, which is <λfp, which λ for web is smaller than λwp, and the section is compact.
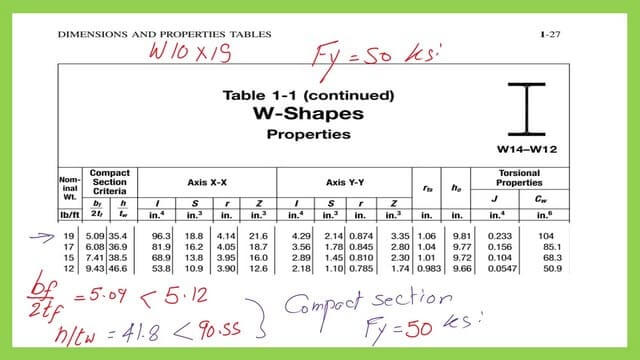
For the Mult, we will adjust due to the superimposed load, the weight of the beam (19 lb/ft), and the final Mult=77.14 ft. kips. The Φb*Mn=81.00 Ft.kips >Mult. The compact section is the last step in designing a steel beam under Fy=50 ksi. This is the end of part 1, which will be followed by part 2.

Here is the link for post 9A, the second part.
Here is the link for Chapter 8 – Bending Members.
This links to the next post, 10-lateral-torsional buckling for steel beams.

