Last Updated on January 2, 2026 by Maged kamel
Moment of inertia Iy-at Cg for a triangle.
Procedure to find the Moment of inertia Iy-at Cg for a triangle.
1-To calculate the Moment of inertia Iy-at Cg or Iyg, we must first estimate the x-bar of the triangle, which is the distance from the triangle’s center of gravity to the Y-axis.

How do we get the X-bar distance for the triangle?
2-To get the x̅ bar distance from the centroid of the triangle to the Y-axis, by using the first moment of area expression, estimate the A*x̅, which is the area of the triangle that will be equal to A1*x̅1 +A2*x̅2 or the multiplication of first area by x1 its cg from the Y axis plus the product of the second area by its cg distance from same y axis.
The value of the first moment of area for the triangle can be estimated as 1/2(b*h) multiplied by x̅ bar, which is the distance of Cg of the first triangle to the y-axis, where the Y bar passes by the external left edge. The first moment of the area can be expressed as the product of an equal initial area and its CG.
From the y-axis, the Cg distance is equal to 2/3a. The first area is (1/2)* a*h*(2/3)*a, and we add the product of the second area by (2a+b/3). The first moment of area for the second triangle equals (1/2)(b-a)*(h)*(2a+b/3).
Add the sum of the first moments of areas of the right-angle triangles. To calculate the final value of the x bar, divide the estimated sum by the triangle’s area as follows: Please see the following slide images for further information.
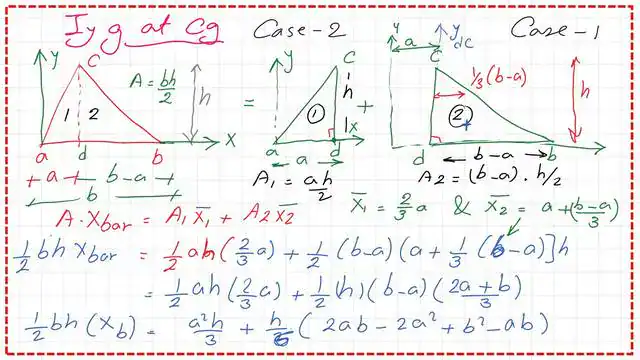
The final x-bar distance for the triangle from the y-axis is 1/3 (a + b). This distance is measured from the Y-axis passing through the left corner.
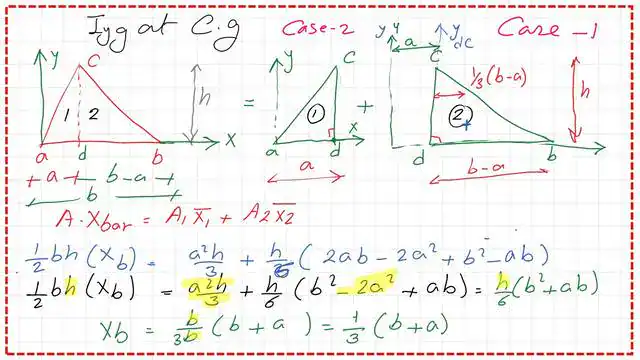
The calculations to get the moment of inertia Iy at the Cg.
3-We can use the parallel axes theory to get the value of the moment of inertia Iy-at Cg-Iyg. We know that Iy=Iyg +(A*xbar^2).
4-To calculate the moment of inertia Iy-at Cg, deduct the product of (Axbar^2) from the value of Iy, which equals (bh/12)(b^2+a^2+ab).
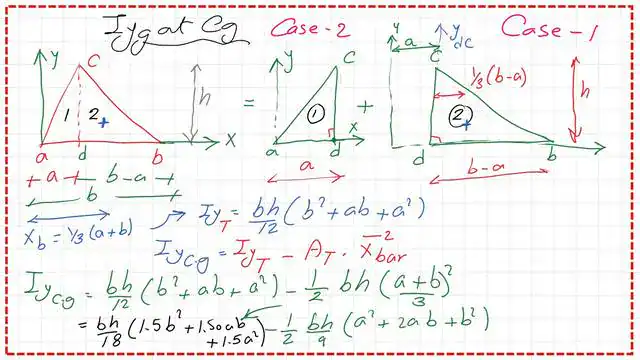
The moment of inertia Iy-at Cg for a triangle is calculated as Iyg=1/18*(b^2-a^2-ab), where a represents the distance from edge point a to point d and b represents the distance between points a and b.
The square of the radius of gyration about the y-axis at the CG can be calculated by dividing the moment of inertia Iy-at Cg, Iyg by the area.
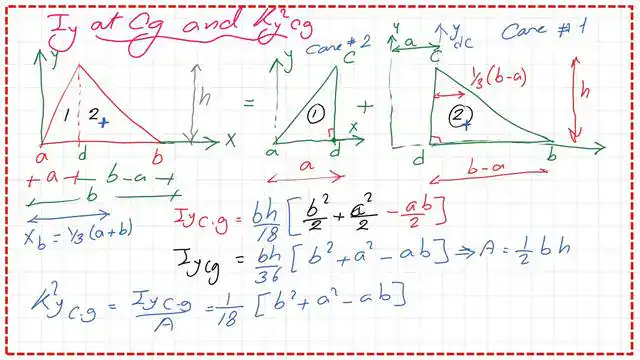
The square of the radius of gyration at the y direction for the triangle at the Cg is equal to 1/18*(b^2+a^2-ab). This is the list of inertia for triangular shapes quoted from the NCEES tables of inertia. From the table, we can see that the calculated moment of inertia Iy at the Cg matches the given value.

You can download and review the content of this post and the previous one through the following pdf file.
For an external resource, the definition of the moment of inertia with solved problems is the 2nd moment of inertia.
This is a link for the next post, Product of inertia Ixy– for the triangle.