Last Updated on January 15, 2026 by Maged kamel
Solved problems for Newton-Raphson method.
The first problem of the two Solved problems for the Newton-Raphson method
Another solved problem for the Newton-Raphson method for root extraction: find the roots of x^3-3x-5=0.
1- starting from the initial point x0=3.00.
First, we try to find that root value by plotting the curve by plugging different values of x,, for example, starting from 0 to 3.0 and negative values from x= -0.50 to -4.00.
We are getting the corresponding y-values. To find roots, we see that the function value between one positive and one negative review lies between x = 2 and x = 2.50.
1-So, our first iteration is selecting x0 value =3.
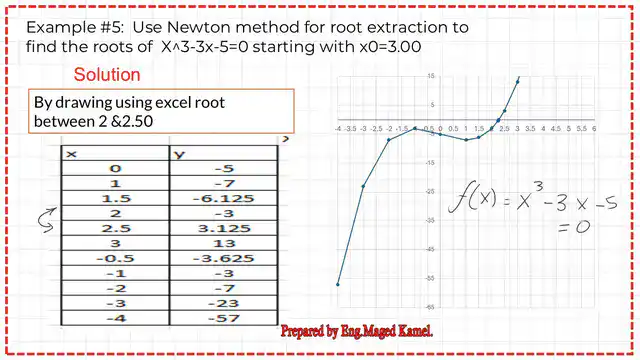
2-Get f(x0=3) and f'(x0=3) f (x) is =x^3-3x-5=0 and f'(x) = 3*x^2-3.
At x0=3 then f(3) = 3^3-3*3-5 =13 and f'(x0=3.00)=3*(3)^2-3=24.00.
3- X1 =3-(13/24)=2.45833.

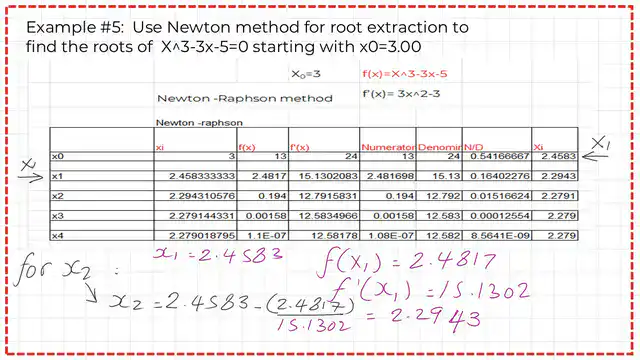
For the second iteration
4—Get the values of f(2.45833) and f'(2.45833). The Excel sheet displays a new value, x2 = 2.2943, along with the corresponding f(x) for each iteration, as shown in the next slide.
We continue iterating until we achieve x4 = 2.279; the error is small.
The second Problem of the two Solved problems for the Newton-Raphson method.
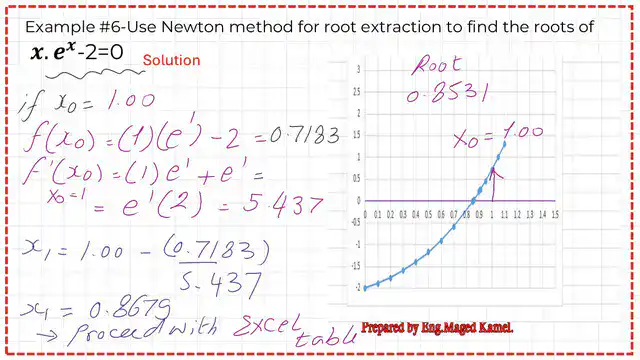
This is the second solved problem of the two Solved problems for the Newton-Raphson method: problem number 6. Use the Newton method for root extraction to find the roots of this function.
Problem number 6: Use the Newton method for root extraction to find the roots of a function.
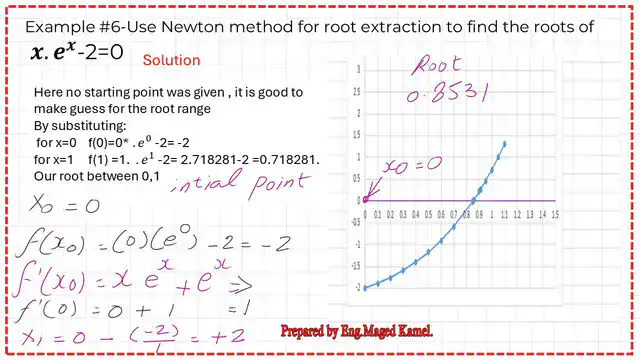
The given function is x*e^x-2=0, and it is required to get the value of x. We do not have the initial point. But when we create an Excel sheet and a graph, we can see that the analytic solution gives x = 0.8531.
The solution is between 0 and 1. We evaluate f'(0), which will be equal to 1, the value of x2 based on the Newton-Raphson method will be equal to +2. Please refer to the following slide image for more details.
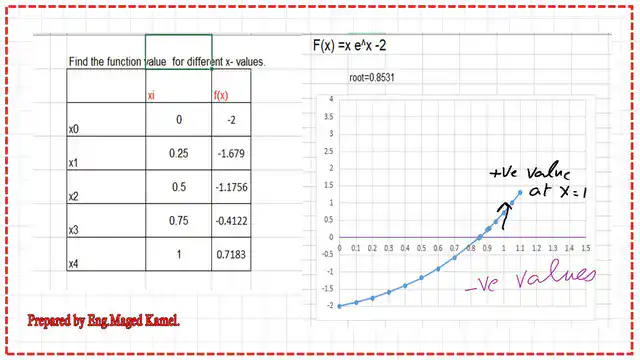
1-We can make a table: we put different values of X and find the corresponding values of our function to locate the exact X value.
Our initial point x0 = 0.
2-We’ll find that when we plug X=0, then (0*e^0)-2, we get -2. For x = 1, f(x) = 0.718251, indicating that the root lies between 0 and 1
3-For the next point where x=0.25, we get (-1.678994).
4-For x=0.50, we get -1.1756.
5- For x=0.750, we get. (-0.4122).
6- For x=1, we get +0.7183.
Between x=0 and x=1.0, for x=0 gives a minus, and for x=1 gives a positive value. Please refer to the following slide image.
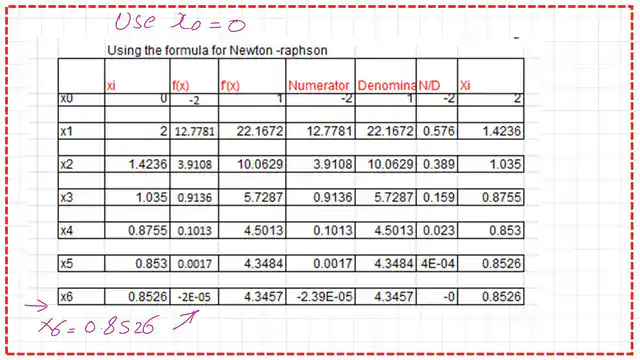
So, our root should exist between 0 and 1. You can start at either x = 0 or x = 1. We put X=0 f(0)=(0)*e^0-2=-2.00, for the slope value, check the next relation, it will be=1.
x1=x0-f(x0)/f'(x0)=0-(-2/1)=+2.00.
For f(2), we have the value of 12.778 and the derivative of x at x equals 2, f'(2)=22.167. So X2 will be =+2-f(x1=2)/f'(x1=2).
X2 will be =+2-(12.778/22.16716)=1.4326.
After substitution, we obtain the function value and the derivative. We use the expression of X3=x2- f(x2)/f'(x2), we get x3=1.035.

It is better to calculate using an Excel sheet. This sheet includes a starting point with a selected value followed by a column that represents the function value f(x), another new column for the value of f'(x), a column for the numerator, which I f(x), and the denominator, which is ‘(x), and then a column for the numerator/ denominator.
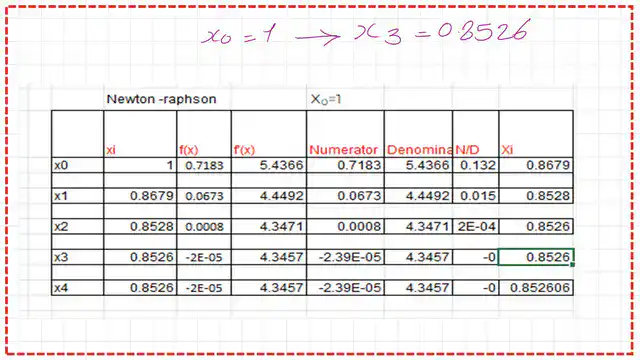
We have two starting points: x0 = 0 and x0 = 1.0. At x6, which is equal to 0.8526, we get a very small value of f(x) that is almost zero. Please refer to the following slide image.
If our starting point x0=1, the value of f(1) will be equal to 0.7183, and the derivative value at x=1 is f'(1)=5.437. The value of x1 will be equal to 0.8679. Please refer to the following slide image.
The following slide includes a snapshot of an Excel table showing the various values of x, and the final x value is 0.8526, for which f(x)=0.
The PDF for this post and the previous post can be reviewed and downloaded via the following document.
The next post is about the Modified-Newton-Raphson method, for which the Newton-Raphson method is modified.
This is a useful link for a numerical analysis calculator.