Last Updated on March 21, 2024 by Maged kamel

Modified Newton-Raphson method.

Introduction to the bracketing method. The bracketing method is a  Numerical method, that represents two values of a function having opposite signs, the root will be in -between.

The modified Newton-Raphson method is another method for root finding.  A simple modification to the previous method of Newton-Raphson was introduced.

I have introduced the Modified Newton Raphson method by applying the new equation for two solved problems. the first solved problem is solved problem 7. I have used the Modified Newton Raphson method to solve. I have introduced an Excel table to show the iterations starting from x0=0.50. that was a part of the video.

Modified Newton Raphon formula.

This formula of the Modified Newton-Raphson method is shown in the next slide image.

Solved problem#7 by using the modified Newton-Raphson Method.

We start by solving problem #7. For the modified Newton Raphson method, I used an Excel sheet to determine the root value of the given f(x)=e^x-3*x^2. I make a table between x and the corresponding value of f(x), by selecting several values of x, starting from 0 to a value of 1.10.

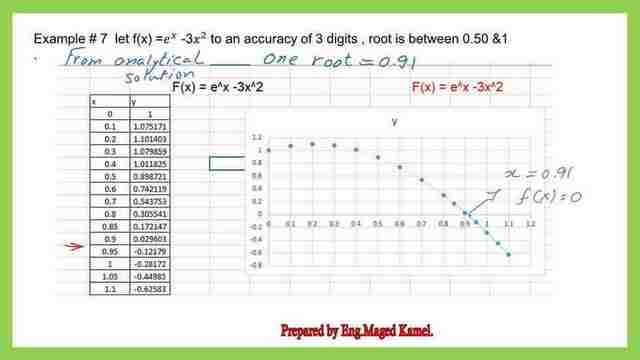
After drawing the function by Excel, the point of f(x)=0 was detected to be at x=0.91 or the root value is at x= 0.91, please refer to the Excel sheet. at an initial point of 0.50, it is required to estimate the root point, the steps are as follows:

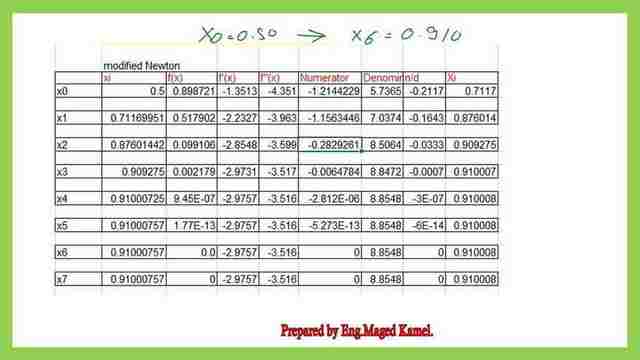
1- Estimate f(xi),f'(xi) , f’^2(xi) and f”(xi) at the starting point of xi=0.50 for an initial i=0.

2- Substitute at xi=0.50 and get the values for f (0.50), f'(0.50) & f’^2(0.50) and f”(0.50) and get the value of x1, it will be=0.7117.

 3- Substitute at x1=0.7117 and get the values for f (0.7117), f'(0.7117)  & f’^2(0.7117)  and f”(0.71112), now we consider i=1, we want to get the x value at I when=2. The value of x2 will be=0.876.

4-Continue the process till x converges to 0.91 as shown in the next table. the next slide image shows the values of x starting from x0=0.50 to x1=0.711699, then x2=0.87601, then x3=0.909275, x4=0.91000, and then x5=0.91000. Check the f(x)=0.

This is the PDF file used for the illustration of this post.

The next post is 7A- Solved problem-8 by Modified Newton-Raphson method

This is a useful link for a numerical analysis calculator.